Chapter 9
Optics, Botany, and the Fibonacci Numbers
As we shall soon see, the Fibonacci numbers even make their way into situations in the natural sciences.
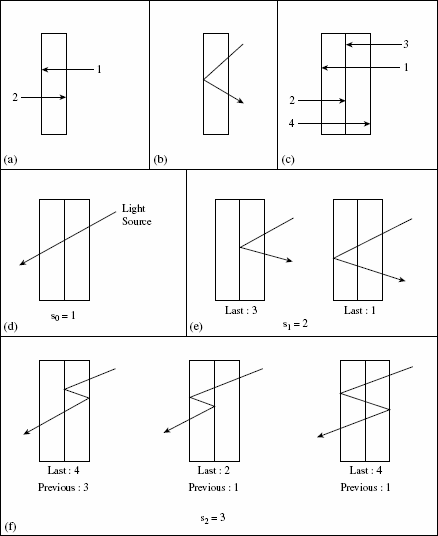
Example 9.1: The following application was introduced in Reference [43] and then solved in Reference [42]. In the science of optics, the branch of physics where one investigates the propagation of light, another instance of the Fibonacci numbers arises. Start by considering a glass plate with two reflective faces, as shown in Fig. 9.1(a). Here Face 1 is the face on the left side of the glass plate, while Face 2 is the face on the right side. In Fig. 9.1(b), we see a single reflection (or change in direction) that occurs at Face 1, when we view this glass plate from the side.
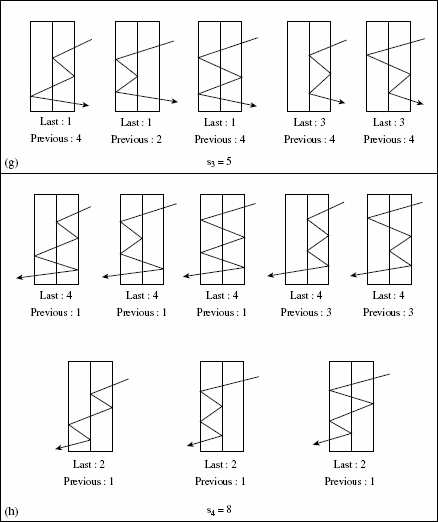
If we now place two such plates back-to-back, as in Fig. 9.1(c), then we have four reflecting faces. Faces 1 and 2 belong to the plate on the left; Faces 3 and 4 belong to the plate on the right. When a light ray falls on this stack of two glass plates, let sn count the number of different paths the ray can take when it is reflected n times, where n ≥ 0. For example, in Fig. 9.1(d), we see the case where there are no reflections, so there is only one possible path and s0 = 1. Part (e) of Fig. 9.1 shows us the two different paths that can occur ...