Fibonacci and Catalan Numbers: An Introduction

Chapter 13

The Lucas Numbers: Further Properties and Examples

At this point we have seen many examples where the Fibonacci numbers arise—and there are still more to come. In addition, in the text and, especially, in the exercises, we found that there are numerous properties that this number sequence exhibits. The Lucas numbers likewise exhibit many interesting properties. In fact, now that we are aware of both of these number sequences, we find that there are some properties interrelating the two sequences. Our next example will provide some of these properties. Many more appear in the exercises for this chapter.

Example 13.1: Previously, in Example 12.5, we let i_n count the number of independent sets of vertices for a path on n vertices and c_n the number of independent sets of vertices for a cycle on n vertices. In that example we learned that

Since c_n turned out to be the Lucas number L_n and i_n = F_n+2, this result translates into the following:

Property 13.1:

And from this the next property follows.

Property 13.2:

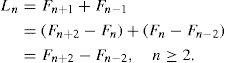
This second property can be used to provide additional examples where the Lucas numbers arise:

i. In Example 6.2 we learned that the number of compositions of n, where ...