Fibonacci and Catalan Numbers: An Introduction

Chapter 14

Matrices, The Inverse Tangent Function, and an Infinite Sum

Now the time has come to introduce some fundamental ideas from linear algebra into our discussion.

Let us start with the matrix

Properties of this matrix were investigated in 1960 by Charles H. King in his Master's thesis at what was, at that time, the San Jose State College in California.

Computing Qⁿ for n = 2, 3, 4, and 5, we arrive at the following:

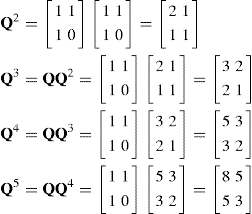
It appears that the entries in these matrices are Fibonacci numbers, since

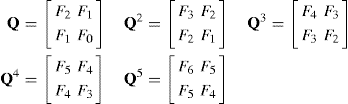
and these results suggest the following.

Theorem 14.1:

For and n ≥ 1,

This theorem can be established by the Principle of Mathematical Induction. We leave this for the exercises at the end of this chapter.

Our next results will follow from the following properties of determinants.

For any square matrix A, we let det (A) denote the determinant of A. Then if A and B are two k × k matrices, we have

1. det (AB) = det (A) det (B)

2.

3. det (A^m+n) = det (A^mAⁿ) = det (A^m) det (Aⁿ)

With these properties ...