Fibonacci and Catalan Numbers: An Introduction

Chapter 18

Historical Background

In 1751, in a letter to the Prussian mathematician Christian Goldbach (1670–1764), the prolific Swiss mathematician Leonard Euler (1707–1783) conjectured a method for counting the following geometric situations.

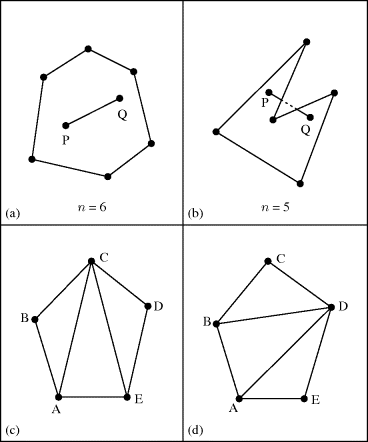
Start with a polygon of n (≥ 3) sides. Such a polygon is called convex if whenever P and Q are two points in the interior of the polygon, then all points on the segment PQ are also in the interior of the polygon—as shown, for example, for the convex hexagon in Fig. 18.1(a) on p. 148. In Fig. 18.1(b), the pentagon shown is not convex, for some of the points on the segment PQ are in the exterior of the pentagon.

Now consider the convex pentagon in Fig. 18.1(c). Here we have triangulated the interior of the pentagon by drawing the two diagonals AC and CE, which do not intersect within the interior of the pentagon. Part (d) of Fig. 18.1 provides a second such triangulation of the interior of the convex pentagon, this time by the diagonals AD and BD.

Figure 18.1

Euler was concerned with determining T_n, the total number of ways one can draw n − 3 diagonals within the interior of a convex polygon of n sides (for n ≥ 3) so that no two of the diagonals intersect within the interior of the polygon, and the interior of the polygon is triangulated into n − 2 triangles. He calculated T_n for the first few small values of n and considered the ratio