Chapter 25
Partial Orders, Total Orders, and Topological Sorting
In Example 13.2, we were introduced to a special type of binary relation on a set A—namely, the notion of the partial order. Furthermore, when the set A is finite, we found that a partial order on A could be studied by means of its Hasse diagram.
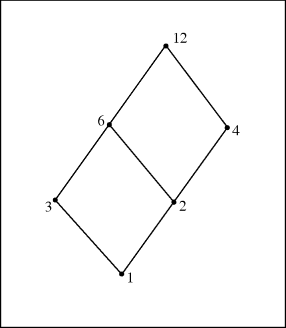
Let us recall these ideas for the set A of all (positive integer) divisors of 12. Hence A = {1, 2, 3, 4, 6, 12} and here the relation 
is defined on A by 
(that is, x is related to y) when x divides y. (Recall that we may also write 
in place of 
.) The Hasse diagram for this partial order is shown in Fig. 25.1.
Continuing, the following ideas will prove useful.
Definition 25.1: For a partial order 
on a set A [often denoted by the pair 
], an element x A is called maximal ...
