Chapter 32
Staircases, Arrangements of Coins, The Handshaking Problem, and Noncrossing Partitions
Even more examples, where the Catalan numbers come to the forefront, will be presented in this chapter. As we did in the previous chapter, here we shall use the nonlinear recurrence relation in Eq. (29.1) to verify that these new examples are counted by the Catalan numbers.
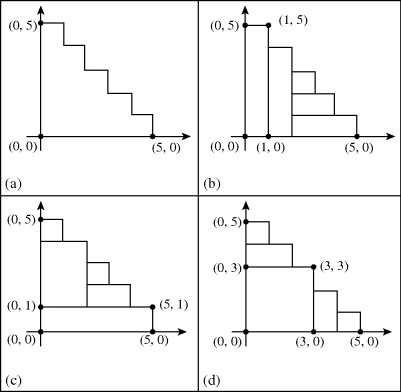
Example 32.1 (Staircases): Consider the five-step staircase shown in Fig. 32.1(a). We are interested in constructing this staircase using five rectangles. In parts (b), (c), and (d) of Fig. 32.1 we find three of the ways this can be accomplished.
Looking at the staircase in Fig. 32.1(b), we find that if we remove the vertical rectangle with corner point (1, 5), then the remaining four rectangles provide a way to construct a four-step staircase from four rectangles. Likewise, in Fig. 32.1(c), upon removing the horizontal rectangle with corner point (5, 1), the four rectangles pictured above it also provide a way to construct a four-step staircase from four rectangles. Finally, in Fig. 32.1(d), we find a square with corner points (0, 0), (0, 3), (3, 3), (3, 0). To the right of this square is one of the (two) ways to construct a two-step staircase using two rectangles, and above this square is the other way to construct such a staircase. In general, we see how the rectangle with (0, 0) as one of its corner ...