Fibonacci and Catalan Numbers: An Introduction

Chapter 36

One Final Example?

As we did in Chapter 17 at the end of Part One, we now want to consider an example where the beginning pattern of results suggests the Catalan numbers—when it is not! This will emphasize one last time that in order to claim that a new example is truly counted by the Catalan numbers, we must either (i) set up a one-to-one correspondence with an example that is known to be counted by the Catalan numbers, or (ii) obtain a recurrence relation like the one in Eq. (29.1), remembering to check the initial condition.

To drive this point home, consider the following:

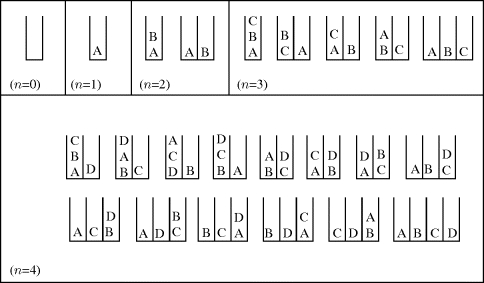
Example 36.1: For n ≥ 0, start with n distinct objects and distribute them among at most n identical containers. Do this, however, while adhering to the following conditions:

1. Do not place more than three objects in any one container.

2. Do not be concerned about how the objects in any given container are arranged.

We shall let d_n count the number of these distributions, for n ≥ 0. From the results in Fig. 36.1, we find that

Figure 36.1

So it appears that we have come upon another situation that is counted by the Catalan numbers. Not so fast! Unfortunately, 297 the suggested pattern does not continue and one finds, for instance, that

The distributions given here were studied in Reference ...