Fibonacci and Lucas Numbers with Applications, Volume 1, 2nd Edition

FIBONACCI AND LUCAS IDENTITIES

Mathematics is the music of reason.

–James Joseph Sylvester (1814–1897)

Both Fibonacci and Lucas numbers satisfy numerous identities. Many were discovered centuries ago. In this chapter we will explore several fundamental identities.

We will begin with a few summation formulas. Exercise 2.10, for example, required that we conjecture a formula for the sum . In doing so, we notice an interesting pattern:

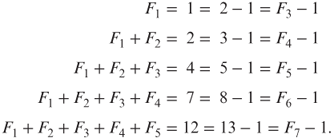
Following this pattern, we conjecture that .

We will now state this as a theorem, and then establish it in two different ways. See Exercise 5.21 for a third method.

A popular technique that is useful in dealing with finite sums is a telescoping sum. A sum of the form is a telescoping sum. It is easy to show that . This will come in handy in establishing the conjecture.

Theorem 5.1 (Lucas, 1876)

5.1

Proof

By the Fibonacci recurrence we have