PASCAL'S TRIANGLE
We will see in this chapter how Fibonacci numbers can be extracted from Pascal's triangle. In addition, we will derive a host of Fibonacci and Lucas identities involving binomial coefficients.
We will begin with a brief discussion of binomial coefficients, which are coefficients occurring in the binomial expansion of 
. The term binomial coefficient was introduced by the greatest German algebraist Michel Stifel (1486–1567).
The earliest known occurrence of binomial coefficients can be traced back to a tenth-century commentary by the Indian mathematician Halayudha on Pingala's Chandas Shastra; interestingly, it also contains a discourse on what is now called Pascal's triangle (called Meru Prastara). Bhaskara (1114–1185?) gives a concise discussion of binomial coefficients in his 1150 classic work Leelavati.
11.1 BINOMIAL COEFFICIENTS
Let n and k be nonnegative integers. The binomial coefficient 
is defined by
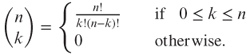
It is also denoted by and . Read as “n choose ...
Get Fibonacci and Lucas Numbers with Applications, Volume 1, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
