HOSOYA'S TRIANGLE
In 1976, H. Hosoya of Ochanomizu University, Tokyo, introduced an interesting triangular array H; see Figure 15.1 [332]. It is closely linked to Fibonacci numbers. We call it Hosoya's triangle. The array is symmetric about the vertical line through the middle, and the top two northeast and southeast diagonals consist of Fibonacci numbers. We can obtain every interior element by adding the two immediate neighbors along the northeast and northwest diagonals; for example, 
.
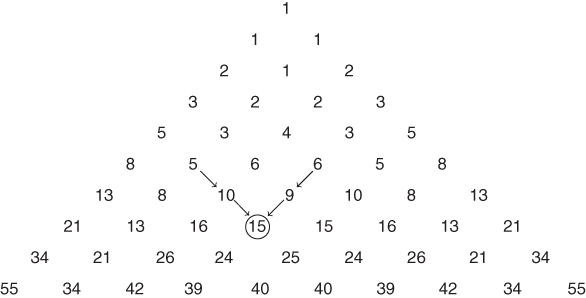
Figure 15.1 Hosoya's triangle H.
15.1 RECURSIVE DEFINITION
We can define the array H recursively, where 
denotes the element in row n and column j:
where 
and 
.
Since , where and , it ...
Get Fibonacci and Lucas Numbers with Applications, Volume 1, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
