CONTINUED FRACTIONS
Recall from Chapter 16 that the sequence of ratios 
of consecutive Fibonacci numbers approaches the golden ratio 
as 
. Interestingly, we can employ these ratios, coupled with Fibonacci recurrence, to generate fractional numbers of a very special nature, called continued fractions1 . The English mathematician John Wallis (1616–1703) coined the term continued fractions. Some continued fractions have finite decimal expansions, while others do not. We will now begin our pursuit with some basic vocabulary and a few characterizations of continued fractions.
19.1 FINITE CONTINUED FRACTIONS
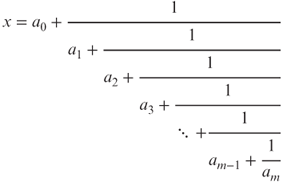
A finite continued fraction is a multi-layered fraction of the form
where each 
is a real number; 
; and . The numbers are the partial quotients of the finite continued fraction. ...
Get Fibonacci and Lucas Numbers with Applications, Volume 1, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
