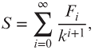FIBONACCI AND LUCAS SERIES
In this chapter, we study the convergence of some interesting Fibonacci and Lucas series, and evaluate them when convergent.
24.1 A FIBONACCI SERIES
To begin with, suppose we place successively every Fibonacci number 
after a decimal point, so its units digit falls in the 
st decimal place. The resulting real number, to our great surprise, is the decimal expansion of the rational number 
. Be sure to account for the carries:
that is, 
. F. Stancliff discovered this result in 1953 [537].
To establish this fact, we need to study the convergence of the Fibonacci series
where k is a positive integer.
Suppose the series converges. Then, by Binet's formula,
Notice that the denominator of the RHS of equation (24.3) is the characteristic polynomial of ...
Get Fibonacci and Lucas Numbers with Applications, Volume 1, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
