Finance, Economics, and Mathematics

Chapter 34A Conditional Law of Large Numbers

Annals of Probability, 8(1) (1980), 142–147.

Abstract

It is shown that, when conditional on a set of given average values, the frequency distribution of a series of independent random variables with a common finite distribution converges in probability to the distribution which has the maximum relative entropy for the given mean values.

Introduction

In statistical mechanics and other areas of physics, empirical distributions in the phase space conform in many circumstances to the distribution maximizing the entropy of the system subject to its constraints. The constraints are typically in the form of specified mean values of some functions of phase. If denotes the probability distribution over the state space, the constraints on p take the form

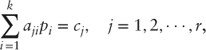
and the maximum entropy distribution is the one that maximizes the entropy function

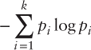
subject to the constraints.

A principle stating that the empirical distribution possesses the maximum entropy within the restrictions of the system is due to Gibbs (1902). As a special case, he proposed the so-called canonical distribution as a description of systems subject to a single constraint that the average ...