Financial Derivative and Energy Market Valuation: Theory and Implementation in MATLAB

Chapter 12: Fourier Transform

12.1 Introduction

The Fourier transform (FT) is a major pillar of mathematics, as numerous calculations and derivations are greatly simplified by recasting the problem into the Fourier space. The discrete version of the FT allows uncomplicated digital translation between the time and frequency domains. The advent of the fast Fourier transform (FFT) in the 1960s greatly accelerated the computation speed of the transform and is arguably the most important applied mathematics development of the 20th century. This chapter starts with an introduction to the theory of the FT. The remainder of the chapter discusses the structure and application of the discrete Fourier transform (DFT), FFT, chirp z transform, Bluestein FFT, and FrFFT (fractional FFT).

12.2 Basic Fourier Transform Equations

The FT and the inverse FT are a complementary mathematical pair that allows the equivalent information to be represented in and transferred to the time domain or the frequency domain. The FT extracts the frequency components from a time or space signal by

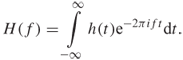
The inverse FT extracts the time or space data from the set of frequency components by

The frequency f measured in cycles ...