Financial Derivative and Energy Market Valuation: Theory and Implementation in MATLAB

Chapter 14: Application of Characteristic Functions

14.1 Introduction

This chapter commences by providing the mathematical link between a characteristic function and its corresponding probability density function (PDF) and cumulative distribution function (CDF). These relationships are used in the generation of a PDF or CDF for any reasonable characteristic function. Proper formatting of the numerical procedure allows the use of efficient fast Fourier transform (FFT) or fractional fast Fourier transform (FrFFT) routines. Similar numerical techniques can be used to fit the parameters of a particular characteristic function to a set of asset prices.

14.2 Levy Theorem

The Fourier transform of the real-space PDF, , is the characteristic function, , as given by

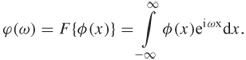
By symmetry, the PDF can be recovered by the inverse Fourier transform of the characteristic function as given by

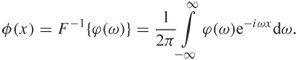
The probability of finding at random variable in the interval (−∞,x) drawn from an arbitrary distribution is the CDF as ...