Financial Economics

WEB-APPENDIX L

SOME ELEMENTARY CONCEPTS INVOLVING PROBABILITY

In this appendix, we summarize the probability concepts we rely on throughout this book. We present them in the context of discrete probability distributions, for example:

rp	Probability
−0.10	0.20
0.00	0.40
0.10	0.40

L.1 PROPERTIES OF THE EXPECTED VALUE OF A RANDOM VARIABLE

We first look at three useful properties of expected values:

Property 1:	The expected value of a constant is that constant. In particular, we shall make considerable use of the notion throughout the book of a risk-free rate of return rf; thus, E(rf) = rf.
Property 2:	The expected value of a constant times a random variable is the constant times the expected value of that random variable. In particular, if xi is the proportion of a portfolio invested in security i and ri is its return, then E(xiri) = xiE (ri).
Property 3:	The expected value of a sum equals the sum of the expected values. In particular, suppose a portfolio consists of two securities, 1 and 2; then E(rp) = E(x1r1) + E(x2r2) = x1E(r1) + x2E(r2). This property is quite general and applies also to sums of functions of random variables.

L.2 MEASURES OF DISPERSION FOR RANDOM VARIABLES

We next look at measures of dispersion for random variables, defining first the variance,

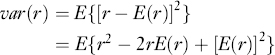
Since the term E(r) inside the braces can be treated as a constant,

We then define standard ...