Financial Markets and Trading: An Introduction to Market Microstructure and Trading Strategies

APPENDIX A

Probability Distributions

Probability distributions are used for describing the statistical properties of a financial time series. While many classical theories are based on the normal (Gaussian) distributions, it has been well documented that empirical data may follow other distributions, too. Here, an overview of probability distributions discussed in this book is provided. For a more detailed description of the material, readers can consult definitive probability courses (e.g., Ross 2007).

BASIC NOTIONS

Consider a random variable (or variate) X. The probability density function f(x) defines the probability to find X between a and b:

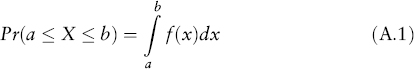
The probability density must satisfy the normalization condition

where the interval [X_min, X_max] is the range of all possible values of X. We shall omit the integration limits when they cover the entire range of possible values. Several distributions widely used in finance are listed in the next section.

Another way of describing random variables is to use the cumulative distribution function:

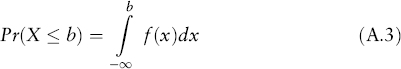
Obviously,

Two characteristics are used to describe ...