Financial Modeling with Crystal Ball and Excel, + Website, 2nd Edition

CHAPTER 4

Selecting Crystal Ball Assumptions

This chapter reviews basic concepts of probability and statistics using graphics from Crystal Ball’s distribution gallery, a portion of which is shown in Figure 4.1. If you have not had a class in basic probability and statistics at some point in your life, or you need a refresher on these topics, consult a business statistics textbook such as Mann (2010). This chapter is intended to show the basics of how to specify probability distributions to be used as stochastic assumptions with Crystal Ball.

FIGURE 4.1 The basic distributions listed in Crystal Ball’s Distribution Gallery.

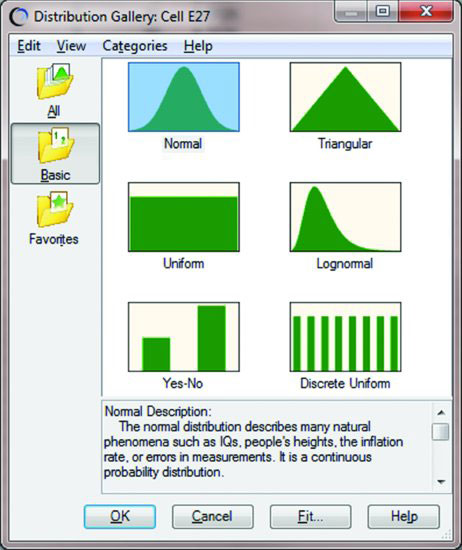
Version 11.1 of Crystal Ball has 22 distributions from which to choose when defining assumptions. To see them, click the All button at the upper left of the distribution gallery. Six basic distributions are described here along with the binomial distribution.

4.1 CRYSTAL BALL’S BASIC DISTRIBUTIONS

4.1.1 Yes-No

Probabilists named the Bernoulli distribution in honor of Jacob Bernoulli, who showed analytically around the year 1700 the truth of the intuitive notion that when a fair coin is tossed repeatedly, it will come up heads about 50 percent of the time. It is perhaps the simplest of all probability distributions. The random variable Y has the Bernoulli distribution if it can take only one of two possible values, y = 0 or y = 1. The value y = 1 is called a ...