Chapter 11
Longdated FX
There are two things I want to talk about in introducing this chapter – the growing importance of interest rate risk as FX option maturities increase and the fact that we’ve been using nontradeables as quasi-numeraires for much of this book. Both are of crucial importance for longdated FX option pricing.
Let Pd(0, T) denote the price today (i.e. Pd(t, T) with t=0) of a domestic zero coupon bond with maturity T. We already know that the value of an ATMF option (see Figure 11.1) is approximately 
, in a Black–Scholes world at least. Consequently, the vega is just 
and scales as the square root of T. In contrast, the interest rate risks, i.e. the rhos, scale linearly in T. One can verify this by setting K = F in (2.67) and differentiating with respect to either rd or rf.
Figure 11.1 Vega and rho profiles for ATMF options
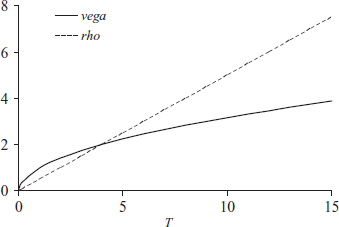
What this means is that for shortdated options, FX volatility, and volatility smile risk in particular, dominates, but for longer dated options, we are increasingly concerned with interest rate uncertainty.
Secondly, the attentive reader will remember that, in accordance with common FX practice, we have been slightly cavalier up to now with our ...
