2Coordinate Systems
In this chapter we discuss three coordinate systems frequently encountered in electromagnetics: Cartesian, cylindrical, and spherical. In each system we define the relevant operations and properties. We conclude by showing the transformations between the systems. These transformations are necessary when deriving the radiation from a Hertzian dipole, as shown in the EMC applications section at the end of this chapter.
2.1 Cartesian Coordinate System
Cartesian coordinate system is shown in Figure 2.1.
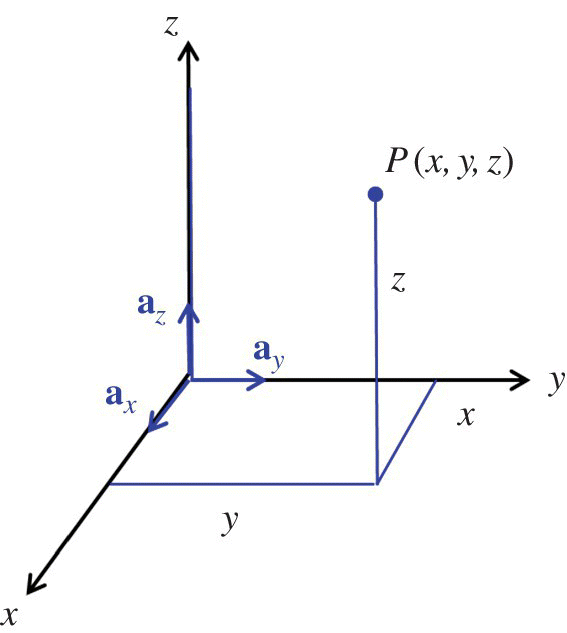
Figure 2.1 Cartesian coordinate system.
Unit vectors in this system, denoted ax, ay, and az, are usually drawn at the origin (but can be drawn at any point in space). They point in the direction of the increasing coordinate variables, and are orthogonal to each other.
A point P can be represented as a triple of numbers
where x, y, and z are called the coordinates of P.
The ranges of the coordinate variables are
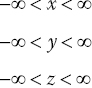
A vector A can be represented as a triple
where Ax, Ay, and Az are called the components of A.
A vector A can be decomposed into a sum of three vectors along ...
Get Foundations of Electromagnetic Compatibility with Practical Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

