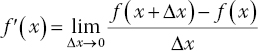Foundations of Electromagnetic Compatibility with Practical Applications

3Vector Differential Calculus

3.1 Derivatives

3.1.1 Basic Definition and Formulas

Derivatives describe the rate at which things change. The derivative is defined as

(3.1)

(We will use this definition when deriving transmission line equations at the end of this chapter.)

Other Notations for Derivatives

Let y be the function of x, that is, y = f (x). We often use the shorthand notation y′ or f ′(x) to denote the derivative of y (Simon, 1982, p. 115). This notation does not indicate the variable with respect to which the derivative is evaluated (y could be a function not only of x but also of other variables). In many applications, it is important to identify that variable. We therefore use the alternative notation or to indicate that derivative of y is computed with respect to the variable x.

Derivative Formulas

Computing derivatives using the definition (3.1) can be tedious. Fortunately, such computations are usually unnecessary because there are derivative formulas that enable us to find the derivatives without computing limits.

Next we will state several useful formulas for derivatives

(3.2a)

(3.2b)

(3.2c)

(3.2d)

(3.2e)

(3.2f)

(3.2g)

(3.2h)

(3.2i)

(3.2j)

Derivative Properties:

(3.3a)

(3.3b)

(3.3c)

(3.3d) ...