Foundations of Electromagnetic Compatibility with Practical Applications

11Frequency‐Domain Analysis

In Chapter 7, we defined the Laplace transformation and used it to obtain the s domain expression for a given time‐domain function, and conversely, we obtained the time‐domain expression from a given s domain function using inverse Laplace transform.

The real power of Laplace transformation in engineering applications emerges when we transform the electrical circuit itself from time domain to s domain and analyze it directly in the s domain. The s domain analysis leads to a definition of a transfer function, and subsequently to the concept of the frequency transfer function, some of the most important concepts in circuit analysis.

In EMC, we are predominantly interested in the sinusoidal steady state and therefore we will focus on the frequency transfer function techniques. We begin by defining the concept a transfer function.

11.1 Transfer Function

The concept of a transfer function is perhaps the most important concept in frequency domain analysis.

A transfer function is defined as the ratio of a Laplace transform of the output Y(s) to the Laplace transform of the input X(s), under the assumptions of zero initial conditions in the circuit (Nilsson and Riedel, 2015, p. 482).

Thus,

(11.1)

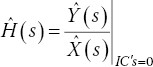
Figure 11.1 shows a typical representation of a circuit in the s domain, used to define the voltage transfer function.

Figure 11.1 Circuit used to define the voltage transfer function. ...