CHAPTER 8 COMPLEX INTEGRATION
In this chapter we will develop techniques and applications of integration for complex functions. The complex integral ∫BAf(z) dz, with z = x + iy, is an integral in the complex plane with respect to the two real variables x and y along a path connecting z = A and z = B. The path need not be a straight line, but can be an arbitrary curve. In this way complex integration is very much like the line integrals one encounters in physics, and this is where the chapter begins. From here the unique properties of complex integrals are developed, with some methods for their evaluation. Finally, we shall see how real definite integrals can often be evaluated using complex integration. The methods are applied to the Fourier transform in this chapter and to related transforms in the next chapter.
8.1 LINE INTEGRALS IN THE PLANE
Review of Real Line Integrals
Line integration is introduced in physics via the definition of work:
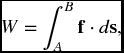
where the vector f is a force field and A and B are the endpoints of the path along which the force acts. The path of integration is specified in parametric form, as a vector-valued function of a single variable. In two dimensions,
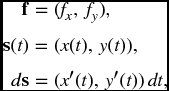
and the integral becomes
with A = (x(tA), y(tA)) and B = (x(tB), y(tB)). Scalar fields f(x, y) are integrated ...
Get Fourier Transforms now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

