Appendix 1 Auxiliary Results from Mathematical, Functional and Stochastic Analysis
A1.1. Special functions
DEFINITION A1.1.– The gamma function is defined by the integral
which converges for any x >0. Here are some basic properties of the gamma function:
- i) the gamma function Γ(x) is positive, continuous and has continuous derivatives of all orders on (0, ∞);
- ii)
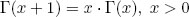 ;
; - iii)
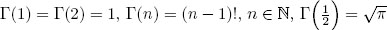 ;
; - iv) the gamma function is logarithmically convex on (0, +∞), i.e. its logarithm is convex on (0, +∞);
- v) the Euler reflection formula is
[A1.2]
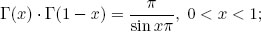
- vi) Legendre’s formula is
[A1.3]
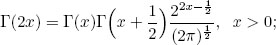
- vii) Gauss’s formula for logarithmic derivative of gamma function has the following form:
where γ is the Euler constant,
DEFINITION A1.2.– The beta function, also called the Euler integral of the first kind, is defined by the ...
Get Fractional Brownian Motion now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

