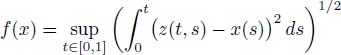Fractional Brownian Motion

1 Projection of fBm on the Space of Martingales

Consider the fractional Brownian motion (fBm) with Hurst index H ∈ (0, 1). Its definition and properties will be considered in more detail in section 1.1; however, let us mention immediately that fBm is a Gaussian process and anyhow not a martingale or even a semimartingale for H ≠ . Hence, a natural question arises: what is the distance between fBm and the space of Gaussian martingales in an appropriate metric and how do we determine the projection of fBm on the space of Gaussian martingales? Why is it not reasonable to consider non-Gaussian martingales? In this chapter, we will answer this and other related questions. The chapter is organized as follows. In section 1.1, we give the main properties of fBm, including its integral representations. In section 1.2, we formulate the minimizing problem simplifying it at the same time. In section 1.3, we strictly propose a positive lower bound for the distance between fBm and the space of Gaussian martingales. Sections 1.4 and 1.5 are devoted to the general problem of minimization of the functional f on L₂([0, 1]) that has the following form:

[1.1]

with arbitrary kernel z(t, s) satisfying condition

(A) for any t ∈ [0, 1] the kernel z(t, ·) ∈ L₂([0, t]) and

[1.2]

We shall call the functional ...