6.8 Two Functions of Two Random Variables
Let X and Y be two random variables with a given joint PDF fXY(x, y). Assume that U and W are two functions of X and Y; that is, U = g(X, Y) and W = h(X, Y). Sometimes it is necessary to obtain the joint PDF of U and W, fUW(u, w), in terms of the PDFs of X and Y.
It can be shown that if (x1, y1), (x2, y2), …, (xn, yn) are the real solutions to the equations u = g(x, y) and w = h(x, y) then fUW(u, w) is given by
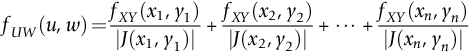 (6.15)
(6.15)
where J(x, y) is called the Jacobian of the transformation {u = g(x, y), w = h(x, y)} and is defined by
Get Fundamentals of Applied Probability and Random Processes, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

