Fundamentals of Computer Graphics, 3rd Edition

i

i

i

i

i

i

i

i

10

Surface Shading

To make objects appear to have more volume, it can help to use shading, i.e., the

surface is “painted” with light. This chapter presents the most common heuristic

shading methods. The first two, diffuse and Phong shading, were developed in the

1970s and are available in most graphics libraries. The last, artistic shading, uses

artistic conventions to assign color to objects. This creates images reminiscent of

technical drawings, which is desirable in many applications.

10.1 Diffuse Shading

Many objects in the world have a surface appearance loosely described as “matte,”

indicating that the object is not at all shiny. Examples include paper, unfinished

wood, and dry unpolished stones. To a large degree, such objects do not have a

color change with a change in viewpoint. For example, if you stare at a partic-

ular point on a piece of paper and move while keeping your gaze fixed on that

point, the color at that point will stay relatively constant. Such matte objects can

be considered as behaving as Lambertian objects. This section discusses how to

implement the shading of such objects. A key point is that all formulas in this

chapter should be evaluated in world coordinates and not in the warped coordi-

nates after the perspective transform is applied. Otherwise, the angles between

normals are changed and the shading will be inaccurate.

233

i

i

i

i

i

i

i

i

234 10. Surface Shading

10.1.1 Lambertian Shading Model

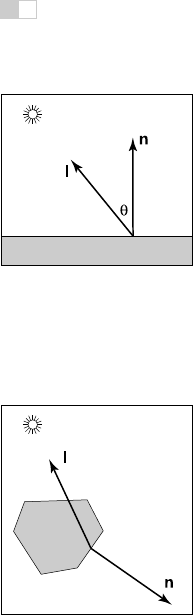
A Lambertian object obeys Lambert’s cosine law, which states that the color c

of a surface is proportional to the cosine of the angle between the surface normal

and the direction to the light source (Gouraud, 1971):

c ∝ cos θ,

or in vector form,

Figure 10.1. The geome-

try for Lambert’s Law. Both

n and l are unit vectors.

c ∝ n ·l,

where n and l are shown in Figure 10.1. Thus, the color on the surface will

vary according to the cosine of the angle between the surface normal and the

light direction. Note that the vector l is typically assumed not to depend on the

location of the object. That assumption is equivalent to assuming the light is

“distant” relative to object size. Such a “distant” light is often called a directional

light, because its position is specified only by a direction.

A surface can be made lighter or darker by changing the intensity of the light

source or the reflectance of the surface. The diffuse reflectance c

r

is the fraction

of light reflected by the surface. This fraction will be different for different color

components. For example, a surface is red if it reflects a higher fraction of red

incident light than blue incident light. If we assume surface color is proportional

to the light reflected from a surface, then the diffuse reflectance c

r

—an RGB

color—must also be included:

Figure 10.2. When a sur-

face points away from the

light, it should receive no

light. This case can be ver-

ified by checking whether

the dot product of l and n is

negative.

c ∝ c

r

n · l. (10.1)

The right-hand side of Equation (10.1) is an RGB color with all RGB components

in the range [0, 1]. We would like to add the effects of light intensity while keeping

the RGB components in the range [0, 1]. This suggests adding an RGB intensity

term c

l

which itself has components in the range [0, 1]:

c = c

r

c

l

n · l. (10.2)

This is a very convenient form, but it can produce RGB components for c that

are outside the range [0, 1], because the dot product can be negative. The dot

product is negative when the surface is pointing away from the light as shown in

Figure 10.2.

The “max” function can be added to Equation (10.2) to test for that case:

c = c

r

c

l

max(0, n · l). (10.3)

Another way to deal with the “negative” light is to use an absolute value:

c = c

r

c

l

|n · l|. (10.4)