Fundamentals of Computer Graphics, 3rd Edition

i

i

i

i

i

i

i

i

2 8

2 8

Spatial-Field Visualization

The topic of visualization was introduced in the previous chapter, together with

visual encodings appropriate for a wide range of types of data. For many visu-

alization applications, the main challenge lies in finding the appropriate spatial

mapping of the data, but in other cases the data comes with a natural mapping.

For instance, a photograph is a set of measured data that has an obvious visual-

ization: simply display it on the screen. However, other ways of displaying the

data may be useful as well, depending on what the user is trying to learn from it.

An X-ray radiograph used to diagnose a broken bone is another example of a 2D

image that is normally displayed directly.

An X-ray is a 2D scalar field: a dataset that describes a function R

2

→ R,

in this case representing a projection of the density of a patient’s body onto a

plane. Other kinds of medical images, such as computed tomagraphy (CT) images

or magnetic resonance images (MRIs), are 2D scalar fields that describe slices

through a patient’s body rather than projections. If many closely-spaced slices

are measured, then the resulting dataset is a 3D scalar field,orvolume dataset,

representing a function R

3

→ R. This type of data can be displayed one slice

at a time, but it also invites perspective or orthographic views that can provide

additional insight into 3D shape.

The importance of scalar fields has led to a number of special techniques and

algorithms, particularly for rendering 3D views of volume data. As with other

kinds of visualization, the primary goal is to map the relevant features of the data

into visual features that play to the strengths of the human visual system.

709

i

i

i

i

i

i

i

i

710 28. Spatial-Field Visualization

28.1 2D Scalar Fields

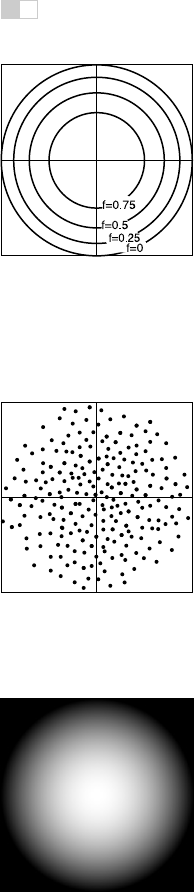
Figure 28.1. A contour

plot for four levels of the

function 1 - x

2

-y

2

.

For simplicity, assume that our 2D scalar data is defined as

f(x, y)=



1 − x

2

− y

2

, if x

2

+ y

2

< 1,

0 otherwise,

(28.1)

over the square (x, y) ∈ [−1, 1]

2

. In practice, we often have a sampled represen-

tation on a rectilinear grid that we interpolate to get a continuous field. We will

ignore that issue in 2D for simplicity.

One way to visualize a 2D field is to draw lines at a finite set of values

f(x, y)=f

i

(shown for the function in Equation 28.1 in Figure 28.1). This

is done on many topographic maps to indicate elevation. Isocontours are excel-

lent at communicating slope, but are hard to read “globally” to understand large

trends and extrema in the data.

Another common way to visualize 2D data is to use small pseudorandom dots

whose density is proportional to the value of the function. This is shown for our

test function in Figure 28.2. Such random density plots are useful for display on

black-and-white media, but are otherwise usually not a good choice for visualiza-

tion. Random density plots look smoother and smoother as more and smaller dots

are used maintaining overall density. As the dot size shrinks below human visual

Figure 28.2. A random

density plot for four levels of

the function 1 - x

2

-y

2

.

acuity, the image looks smooth. This results in a grayscale continuous tone plot

of the function. It is hard for humans to read such plots, because our ability to

detect absolute intensity levels is poor. For this reason, color or thresholding is

often used. This is shown in grayscale in Figure 28.3. Formally, we can specify

such a mapping with just a function g that maps scalar values to colors:

g : R → [0, 1]

3

.

Here [0, 1]

3

refers to the RGB cube. A common strategy is to specify a set of

colors to which specific values map and linearly interpolate colors between them.

A set of colors that increases in intensity and cycles in hue is often used. Such a

set of colors for the domain [0, 1] is

Figure 28.3. A grayscale

density plot of the function

1-x

2

-y

2

.

g(0.00) = (0.0, 0.0, 0.0)

g(0.25) = (0.0, 0.0, 1.0)

g(0.50) = (1.0, 0.0, 0.0)

g(0.75) = (1.0, 1.0, 0.0)

g(1.00) = (1.0, 1.0, 1.0)