Exercise Solutions
Chapter 1
1.1 
and 
. Therefore, expanding the cosine and sine functions and collecting terms, we equate the coefficients of the complex exponentials, and we have c0=a0 and
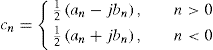
1.2 It is very similar to the autocorrelation function of the random binary waveform.
1.3 
. By the indepedence of x(t) from the sinusoid, we can regroup terms and write
and the result follows.
1.4 We simply take the Fourier transform of Ryy(t), given by (1.97), and by the “modulation” property in Table 1.2, Sy(f) is just Sx(f) shifted/translated by the carrier frequency.
1.5 Let y(t) be the output of the matched filter. Then y(T) is the output of the sampling operation following the matched filter. We have
Thus,
and this is exactly the correlation receiver.
Chapter 2
2.1 Cylindrical: , , and . Spherical: ...
