Game Theory: An Introduction, 2nd Edition

CHAPTER THREE

Two-Person Nonzero Sum Games

But war’s a game, which, were their subjects wise, Kings would not play at.

—William Cowper, The Winter Morning Walk

I made a game effort to argue but two things were against me: the umpires and the rules.

—Leo Durocher

All things are subject to interpretation. Whichever interpretation prevails at a given time is a function of power and not truth.

—Friedrich Nietzsche

If past history was all there was to the game, the richest people would be librarians.

—Warren Buffett

3.1 The Basics

The previous chapter considered two-person games in which whatever one player gains, the other loses. This is far too restrictive for many games, especially games in economics or politics, where both players can win something or both players can lose something. We no longer assume that the game is zero sum, or even constant sum. All players will have their own individual payoff matrix and the goal of maximizing their own individual payoff. We will have to reconsider what we mean by a solution, how to get optimal strategies, and exactly what is a strategy.

In a two-person nonzero sum game, we simply assume that each player has her or his own payoff matrix. Suppose that the payoff matrices are as follows:

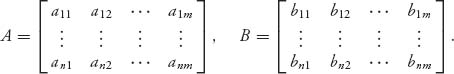
For example, if player I plays row 1 and player II plays column 2, then the payoff to player I is a12 and the payoff to player II is b12. In a zero sum game, ...