Problems
6.25 There are three types of planes (1, 2, and 3) that use an airport runway. Plane 1 needs a 100-yard runway, 2 needs a 150-yard runway, and 3 needs a 400-yard runway. The cost of maintaining a runway is equal to its length. Suppose this airport has one 400-yard runway used by all three types of planes and assume also that only one plane of each type will land at the airport on a given day. We want to know how much of the $400 cost should be allocated to each plane.
6.26 In a glove game with three players, player 1 can supply one left glove and players 2 and 3 can supply one right glove each. The value of a coalition is the number of paired gloves in the coalition.
6.27 Consider the normalized characteristic function for a three-person game:
![]()
Find the core, the least core X1, and the next least core X2. X2 will be the nucleolus.
6.28 Find the fair allocation in the nucleolus for the three-person characteristic function game with
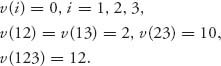
6.29 In Problem 6.12, we considered the problem in which companies can often get a better cash return if they invest larger amounts. There are three companies who may cooperate to invest money ...
Get Game Theory: An Introduction, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

