Appendix A: The Essentials of Matrix Analysis
A matrix is a rectangular collection of numbers. If there are n rows and m columns, we write the matrix as An × m, and the numbers of the matrix are aij, where i gives the row number and j gives the column number. These are also called the dimensions of the matrix. We compactly write ![]() In rectangular form
In rectangular form

If n = m, we say that the matrix is square. The square matrix in which there are all 1s along the diagonal and 0s everywhere else is called the identity matrix:

Here are some facts about algebra with matrices:
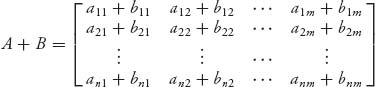

Get Game Theory: An Introduction, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

