GARCH Models, 2nd Edition

Appendix E Solutions to the Exercises

Chapter 1

1. 1.1
   1. 1. (a) We have the stationary solution X _t  = ∑ _i ≥ 00.5 ⁱ (η _t − i  + 1), with mean EX _t  = 2 and autocorrelations ρ _X (h) = 0.5^∣h∣ .
      2. (b) We have an ‘anticipative’ stationary solution
         
         which is such that EX _t  =  − 1 and ρ _X (h) = 0.5^∣h∣ .
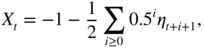
      3. (c) The stationary solution
         
         is such that EX _t  = 2 with ρ _X (1) = 2/19 and ρ _X (h) = 0.5 ^h − 1 ρ _X (1) for h > 1.
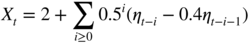
   2. The compatible models are, respectively, ARMA(1, 2), MA(3) and ARMA(1, 1).
   3. The first noise is strong, and the second is weak because
      

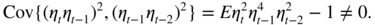
      Note that, by Jensen's inequality, this correlation is positive.

2. 1.2 Without loss of generality, assume 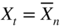for t < 1 or t > n . We have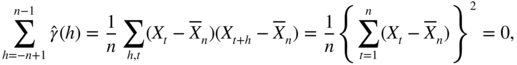
   

   which gives 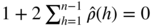, and the result follows.

3. 1.3 Consider the degenerate sequence (X _t ) _{t = 0, 1, …} defined, on a probability space (Ω, 풜, ℙ), by X _t (ω) = (−1) ^t for all