GARCH Models, 2nd Edition

6 Estimating ARCH Models by Least Squares

The simplest estimation method for ARCH models is that of ordinary least squares (OLSs). This estimation procedure has the advantage of being numerically simple, but has two drawbacks: (i) the OLS estimator is not efficient and is outperformed by methods based on the likelihood or on the quasi‐likelihood that will be presented in the next chapters; (ii) in order to provide asymptotically normal estimators, the method requires moments of order 8 for the observed process. An extension of the OLS method, the feasible generalised least squares (FGLS) method, suppresses the first drawback and attenuates the second by providing estimators that are asymptotically as accurate as the quasi‐maximum likelihood under the assumption that moments of order 4 exist. Note that the least‐squares methods are of interest in practice because they provide initial estimators for the optimisation procedure that is used in the quasi‐maximum likelihood method.

We begin with the unconstrained OLS and FGLS estimators. Then, in Section 6.3, we will see how to take into account positivity constraints on the parameters.

6.1 Estimation of ARCH( q ) models by Ordinary Least Squares

In this section, we consider the OLS estimator of the ARCH( q ) model:

6.1

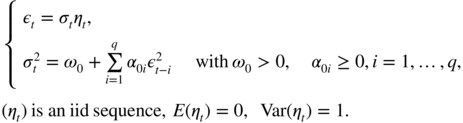
The OLS method uses the AR representation on the squares of the observed process. No assumption is ...