Appendix C
Solutions to the Exercises
Chapter 1
1.1 1. (a) We have the stationary solution Xt = Σi≥0 0.5i(ηt−i+ 1), with mean EXt = 2 and autocorrelations ρx(h) = 0.5|h|.
(b) We have an ‘anticipative’ stationary solution
which is such that EXt = − 1 and ρx(h) = 0.5|h|.
(c) The stationary solution
is such that EXt = 2 with ρx(1) = 2/19 and ρx(h) = 0.5h−1 ρx(1) for h > 1.
2. The compatible models are respectively ARMA(1, 2), MA(3) and ARMA(1, 1).
3. The first noise Is strong, and the second is weak because
Note that, by Jensen’s Inequality, this correlation is positive.
1.2 Without loss of generality, assume Xt = ![]() for t < 1 or t > n. We have
for t < 1 or t > n. We have
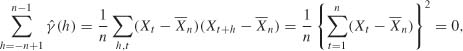
which gives ![]() , and the result follows.
, and the result follows.
1.3 Consider the degenerate sequence (Xt)t=0, 1, … defined, on a probability space (![]() , , ), by Xt(ω) = (−1) ...
, , ), by Xt(ω) = (−1) ...

