Gateways Into Electronics

4

FROM FIELDS TO CIRCUITS

4-1 INTRODUCTION

The concepts of an ideal capacitor or of an ideal inductor are widely used, and rightfully so, because they are fertile abstractions. In this chapter we will look into some aspects of the physics of lumped circuit elements in order to understand the context in which these abstractions are valid. In doing so, we will incidentally lay the groundwork for later discussions on transistors, transmission lines, and noise. To get to the point without hindrance, we will not consider lumped elements containing dielectric or magnetic materials; we will thus deal with metals, resistive materials with permittivity ∊₀, and air (vacuum).

As we proceed, we will see that the range over which lumped elements are ideal is actually quite broad: we might have to do some rethinking beyond 100 MHz, but at 100 kHz we seldom have anything to worry about. More specifically, we will show that a lumped element can be considered ideal only for frequencies such that

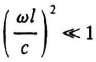
where l is a characteristic dimension of the element. This is not a sufficient condition, but it is certainly necessary. With this condition in mind, we will review Maxwell's equations and see what approximations are valid if it holds.

We will also see that fair representations of physical lumped elements can be obtained by adding corrections—in the form of further ideal elements—to the basic idealized elements. ...