Growth Curve Modeling: Theory and Applications

2

FUNDAMENTALS OF GROWTH

2.1 TIME SERIES DATA

We may view a time series as a set of observations Y_t, t = 0, 1, 2, ..., n, on a variable Y that are indexed in order of time; that is, the Y_t's are measured at different time points or time intervals. Since t is the time index, if our data series starts in, for instance, 1980 and we have observations going to 2005 in one-year intervals, then we can assign a sequence of numbers to order the data points. In this regard, let us designate 1980 as the origin and assign it the value “0.” Then 1981 is assigned the value 1, 1982 is given the value 2, and so on. Hence, we end up with the sequence of numbers 0, 1, 2, ..., 25 as the set of observations on the time variable t. The convenience of this numerical assignment scheme for representing a sequence of years (or weeks, months, etc.) will become evident later on.

2.2 RELATIVE AND AVERAGE RATES OF CHANGE

Given the time series Y_t, t = 0, 1, ..., n, let us define the relative rate of change in Y between periods t−1 and t as

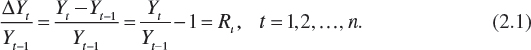
TABLE 2.1 Relative Growth Rates in Y and Growth Relatives

If Y₀ denotes the value of Y at the beginning of period 1 and Y_t represents the value of Y at the end of period t, t = 1, ..., n, then the sequence of relative rates of growth over the entire time span appears in