Growth Curve Modeling: Theory and Applications

6

NONLINEAR REGRESSION

6.1 INTRINSIC LINEARITY/NONLINEARITY

In the classical linear regression model, the multivariate regression hyperplane has the form

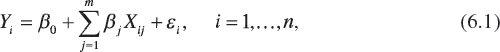
where we have m predetermined explanatory variables or regressors X₁, ..., X_m and ε is a random error term. Here Equation 6.1 depicts a linear regression model since it is linear in the parameters β₀, β₁, ..., β_m. It is assumed that n > p = m + 1 and no exact linear relationship exists between the X_j's, j = 1,..., m.

For fixed X_j's, j = 1,..., m, the population regression hyperplane is specified as the conditional mean of Y given the X_j's or

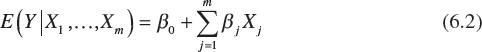
given that E(ε) = 0. Given Equation 6.2,

that is, the population intercept is the mean of Y given that all of the X_j's are set equal to zero. Also,

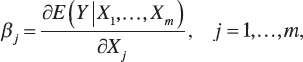
is termed the jth partial regression coefficient; that is, as X_j increases by one unit, the average value of Y changes by β_j units, given that all remaining explanatory variables are held constant. Once the β_k's, k = 0, 1,..., m, are estimated from the sample information, we obtain the sample regression hyperplane

where Ŷ is the estimated value of ...