23
Technical Tools Useful in ALM
À bon cheval, bon gué.
23.1 RISK MEASURES
Nowadays, there are many ways to measure the risk of a portfolio. The approach developed by Markowitz (1952) based on the analysis of variance is still the basis of the risk measurement.
We will start with the presentation of the major risk measures and finish with the presentation of the associated optimization methods.
23.1.1 Variance and standard deviation
Variance is the most simple risk measure in finance. For a random variable X, the mathematical expectation of X is denoted E(X) and the variance V(X). The variance is the mathematical expectation of the square of the difference between X and its mathematical expectation:
![]()
The wider is the distribution of the possible values of X, the higher is the risk.
Since the variance is by construction positive, the standard deviation defined as the square root of the variance is an equivalent risk measure (also called volatility):
![]()
We consider that X has a cumulative distribution function F or a density p:
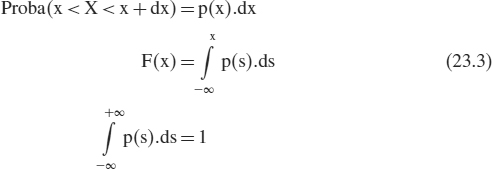
Then the mathematical expectation and the variance will follow:
23.1.2 Value-at-Risk
The Value-at-Risk (VaR) is characterized by a given probability ...
Get Handbook of Asset and Liability Management: From models to optimal return strategies now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

