Handbook of Exchange Rates

5.7 Appendix A: A Formal Test of Hollowing Out

The hypothesis of hollowing out needs to be supported by more than assertion or casual empiricism. In Masson (2001), the hypothesis is formally tested in the context of a Markov-chain model of the transitions between exchange rate regimes. In this model, the probability of moving between the three regimes—fixed, intermediate, and flexible—is assumed to be constant (including the probability of remaining in the current regime). Then, the hollowing out hypothesis can be equated with a test for whether the two polar regimes constitute a closed set—there can be transitions toward them from intermediate regimes and transitions between fixed and flexible, but none toward the intermediate regimes. This hypothesis can be tested on the estimated transition matrix. If true, the hypothesis implies that the long-run distribution of exchange rate regimes, obtained by iterating the Markov chain to infinity, would involve fixed and flexible regimes and zero occurrence of intermediate regimes.

Writing this formally, let the transition probabilities be a matrix P = {p_ij}, with the sum across each row equal to unity. Thus, in the general case, the matrix has the following form:

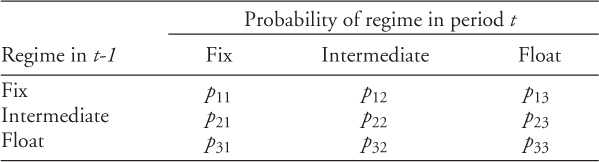
Hollowing out will occur if and only if one or both of the fixed and floating regimes constitute an absorbing state, or if they together constitute a closed set. In either case, ...