Handbook of Game Theory

${\displaystyle \sum _{k=1}^{\tau }{E}_{\tilde{P}}[1-E_{\tilde{P}}[{\sigma }_2(h_2^{t+k})({\widehat{a}}_2)|h_1^{T_1},B]\to 0\text{ as t}\to \infty }$

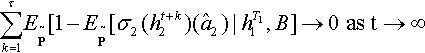
This implies [4.9], since convergence in probability implies subsequence a.e. convergence (Chung, 1974, Theorem 4.2.3).

Using Lemma 4.4, we next argue that on B∩F, player 1 believes that player 2 is eventually ignoring her history while best responding to ${\widehat{\alpha }}_1$. In the following lemma, ε₂ is from [4.6]. The set $A_t(\tau )$ is the set of player 2 t-period histories such that player 2 ignores the next τ signals ...