Handbook of Heavy Tailed Distributions in Finance

$\begin{array}{l} r_{J D}^{*} (i + 1, j_{i + 1}) = r_{J D}^{*} (j_{i + 1}) \\ = {\begin{cases} \begin{matrix} r_{D}^{*} (j_{i}) + Δ_{u} (j_{i}, j_{i + 1}) + μ + γ, & w . prob . \frac{λ}{2} p_{u} (j_{i}), \\ r_{D}^{*} (j_{i}) + Δ_{u} (j_{i}, j_{i + 1}) & w . prob . (1 - λ) p_{u} (j_{i}), \end{matrix} \\ \begin{matrix} r_{D}^{*} (j_{i}) + Δ_{u} (j_{i}, j_{i + 1}) + μ - γ, & w . prob . \frac{λ}{2} p_{u} (j_{i}), \end{matrix} \\ \begin{matrix} r_{D}^{*} (j_{i}) + Δ_{d} (j_{i}, j_{i + 1}) + μ + γ, & w . prob . \frac{λ}{2} p_{d} (j_{i}), \end{matrix} \\ \begin{matrix} r_{D}^{*} (j_{i}) + Δ_{d} (j_{i}, j_{i + 1}), & w . prob . (1 - λ) p_{d} (j_{i}), \end{matrix} \\ \begin{matrix} r_{D}^{*} (j_{i}) + Δ_{d} (j_{i}, j_{i + 1}) + μ - γ, & w . prob . \frac{λ}{2} p_{d} (j_{i}) . \end{matrix} \end{cases} \end{array}$

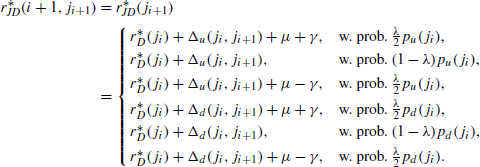
si323_e

Then, the hexanomial tree representing the jump-diffusion process (16) is defined by

$r_{J D}^{*} (i + 1, j_{i + 1}) = r_{J D}^{*} (j_{i + 1}) + α (i + 1),$

for any i = 0,…,M− 1 and $j_{i} \in J_{i} \cap (j_{d}, j_{u})$ .

4 The econometric analysis

4.1 ...

Get Handbook of Heavy Tailed Distributions in Finance now with the O’Reilly learning platform.

O’Reilly members experience live online training, plus books, videos, and digital content from nearly 200 publishers.

Start your free trial

Handbook of Heavy Tailed Distributions in Finance by S.T Rachev

4 The econometric analysis

4.1 ...

Don’t leave empty-handed

It’s yours, free.