April 2015
Intermediate to advanced
1064 pages
33h 41m
English
book
Handbook of Multi-Commodity Markets and Products: Structuring, Trading and Risk Management
by Mark Cummins, Gianluca Fusai, Andrea Roncoroni
Content preview from Handbook of Multi-Commodity Markets and Products: Structuring, Trading and Risk Management
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
CHAPTER 11 An Introduction to Stochastic Calculus with Matlab® Examples
Laura Ballotta and Gianluca Fusai
Given the technical nature of the quantitative applications covered in Part II, we open with a comprehensive introduction to stochastic calculus. Readers who are competent in stochastic calculus are encouraged to proceed and explore the chapters that follow. Those less competent with stochastic calculus will find this chapter beneficial before progressing.
The aims of this chapter are:
- To introduce the concept of Brownian motion.
-
What are W(t) and dW(t)?
-
What are the properties of W(t)?
-
- To explain the meaning of the stochastic differential equation
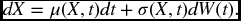
- To explain the meaning of the stochastic integral. For example:
-
To give meaning to
-
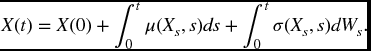
The properties of X(t): distribution, expected value, variance.
-
How to construct a (continuous) martingale.
-
- To explain Itô's formula.
-
For example, how to relate
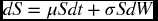
to
-
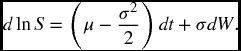
- Examples of common stochastic differential equations:
-
arithmetic Brownian motion;
-
geometric Brownian motion;
-
mean-reverting Gaussian model (Vasicek);
-
mean-reverting ...
-
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.