Hands-On Machine Learning with Scikit-Learn and TensorFlow

Appendix D. Autodiff

This appendix explains how TensorFlow’s autodiff feature works, and how it compares to other solutions.

Suppose you define a function f(x,y) = x²y + y + 2, and you need its partial derivatives and , typically to perform Gradient Descent (or some other optimization algorithm). Your main options are manual differentiation, symbolic differentiation, numerical differentiation, forward-mode autodiff, and finally reverse-mode autodiff. TensorFlow implements this last option. Let’s go through each of these options.

Manual Differentiation

The first approach is to pick up a pencil and a piece of paper and use your calculus knowledge to derive the partial derivatives manually. For the function f(x,y) just defined, it is not too hard; you just need to use five rules:

• The derivative of a constant is 0.

• The derivative of λx is λ (where λ is a constant).

• The derivative of x^λ is λx^{λ – 1}, so the derivative of x² is 2x.

• The derivative of a sum of functions is the sum of these functions’ derivatives.

• The derivative of λ times a function is λ times its derivative.

From these rules, you can derive Equation D-1:

Equation D-1. Partial derivatives of f(x,y)

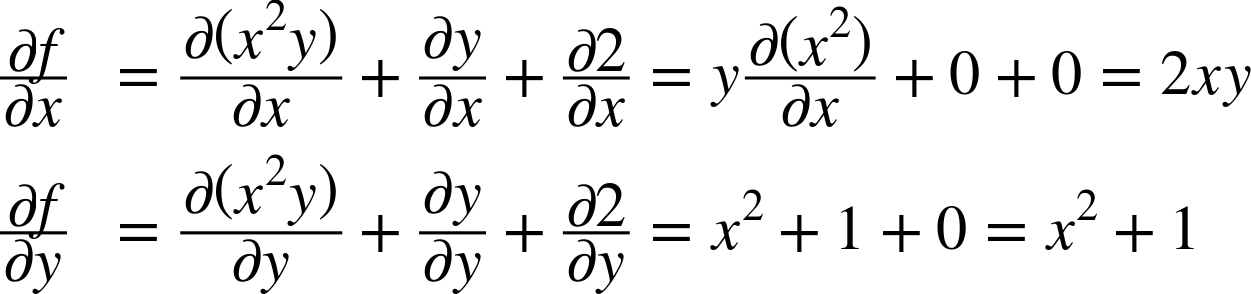
This approach ...