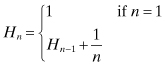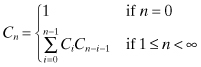Hashing in Computer Science: Fifty Years of Slicing and Dicing

CHAPTER 2

Recurrence and Generating Functions

Standard references on the theory and application of generating functions are [Riordan 1968 and 1980].

2.1 RECURSIONS

A recursion for a sequence a₀, a₁, … is a rule for computing a_n in terms of quantities depend on n and perhaps some of the previous terms a₀, a₁, … , a_n−1.

Examples 2.1.

a) The factorial n! of the integer n may be defined recursively by

b) The harmonic numbers {H_n : 1 ≤ n < ∞} may be defined recursively by

c) The Fibonacci sequence¹ {F_n : 0 ≤ n < ∞} may be defined recursively by

d) The Catalan numbers² {C_n : 0 ≤ n < ∞} may be defined by the recursion

2.2 GENERATING FUNCTIONS

The generating function A(z) of the sequence a₀, a₁, … is the power series

(2.1a)

Whenever we write an infinite series, there is the question of convergence. The series in equation (2.1a) converges provided the radius of convergence . In this ...