triangle properties
Special O
er
60% o!
$750
SCREEN WAREHOUSE
Only slightly damaged, these screens still present a
crystal clear image but with uneveness in the viewable
range to each side.
28 31
30
Web ad f
or the
sp
ecia
l offer
screens
Will the special offer screen still do the job?
The screen is suitable if the viewable range (r) reaches
all the way to the back—but you only have the sides
given on the specification in the ad.
25
28 31
30
r ?
you are here 4 193
What technique from your Geometry Toolbox can help you find
the screen’s viewable distance, r?
Alti
tude
a
2
+ x
2
= 28
2
And this here
a
2
+ y
2
= 31
2
a new tool for your geometry toolbox
What technique from your Geometry Toolbox can help you find
the screen’s viewable distance, r?
The Pythagorean Theorem
It’s the right answ
er, but i
t’s a
lso
a w
orld of pain…so hold tight f
or
a new t
ool for y
our t
oolbox!
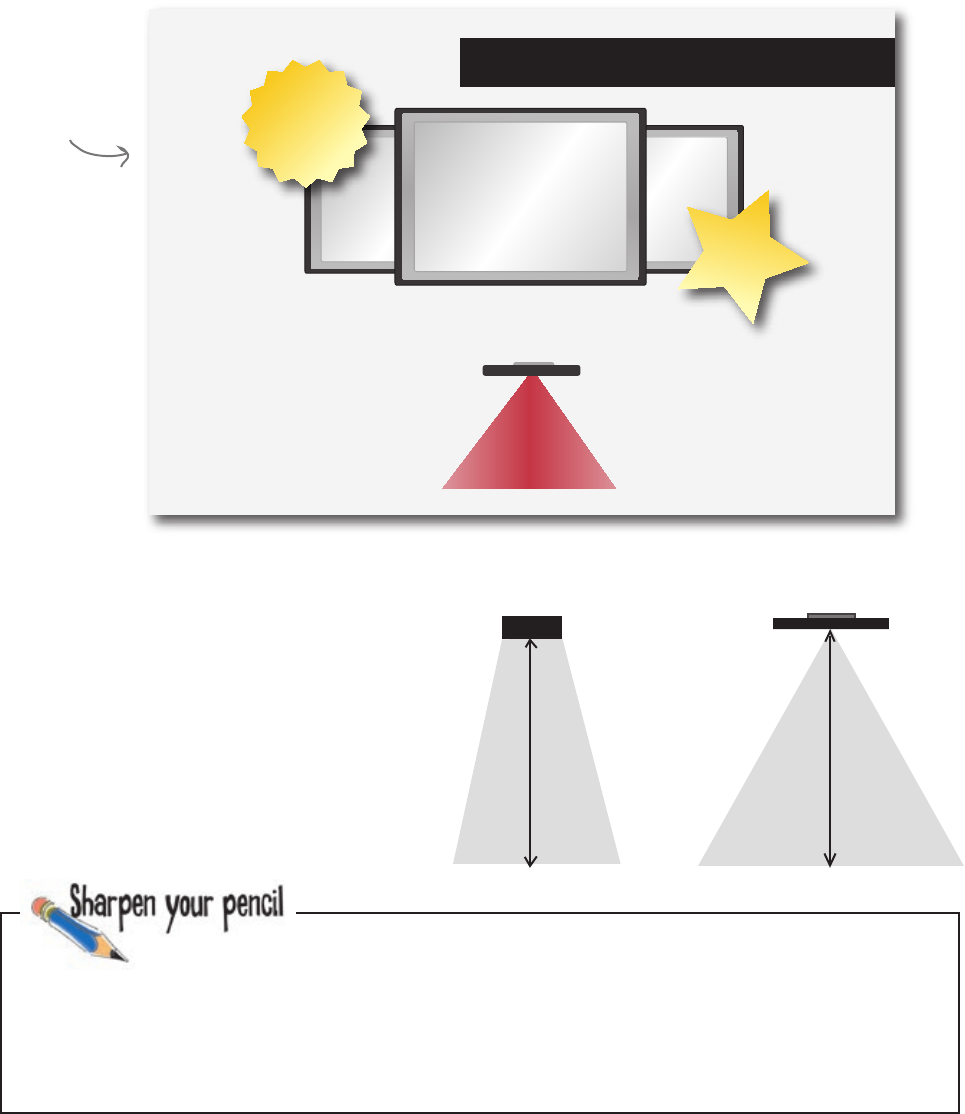
The screen viewing area is a scalene triangle
This means that when you add an altitude, it doesn’t bisect
the base. Instead of creating two nice, neat congruent right
triangles, you get two different right triangles. And you don’t
know the base of either of them!
So w
e’d need to
sol
v
e this her
e
28
31
28
31
a a
All three sides
are different
lengths.
x y
30
The two right triangles still work with the Pythagorean
Theorem, and we know that x and y together make 30 (but
aren’t equal to each other) so we could figure this out with a set
of three simultaneous algebra equations. If that sounds bad,
it kinda is. Don’t go there. But in case you’re tempted, here’s
how it starts out:
Plus, x and y ar
en’t jus
t ha
lf of 30!
a
2
+ x
2
= 28
2
a
2
+ y
2
= 31
2
x + y = 30
(a
2
+ x
2
= 28
2
)
- (a
2
+ y
2
= 31
2
)
3 equations
DANGER
do not cross this line
by subtraction
x
2
- y
2
= 28
2
- 31
2
x + y = 30, so x = (30 - y) (30 - y)
2
- y
2
= 28
2
-31
2
by substitution
Now…expand this out....
194 Chapter 4

triangle properties
Wouldn’t it be dreamy if there was a
way to find the height of a scalene triangle
without simultaneous equations? But I know
it's just a fantasy....
you are here 4 195
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

