
factoring in perimeter
Calculate the perimeters of the two lawns. How does this account
for the difference in time spent on each lawn? What do you think
Edward should do?
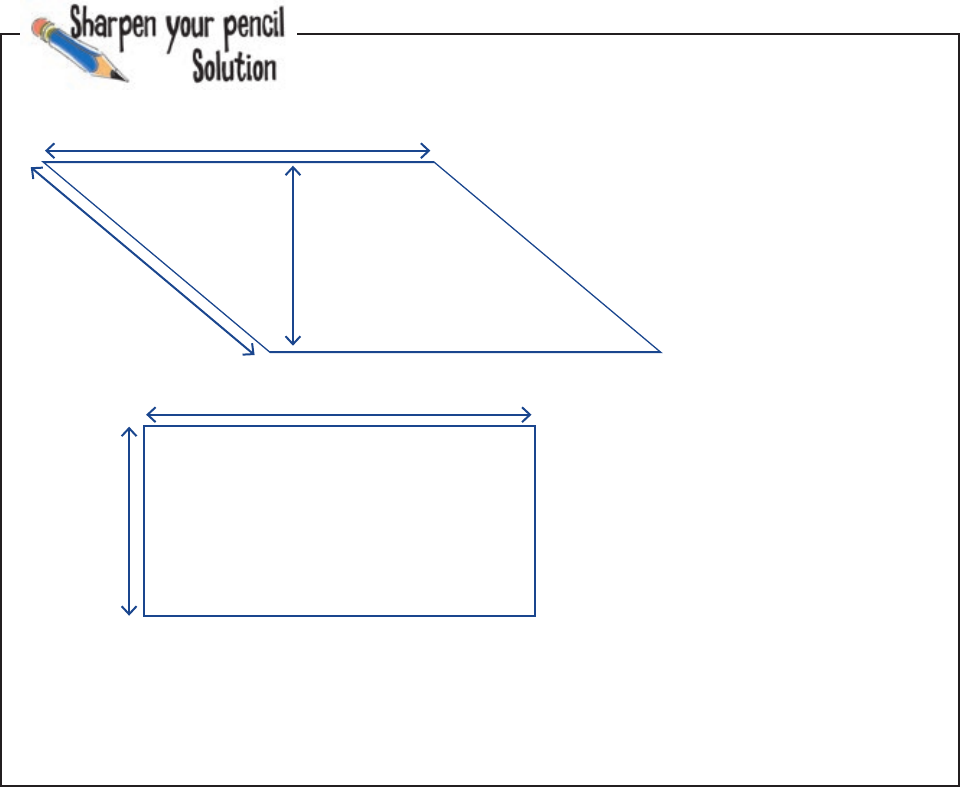
45 meters
16 meters
34 meters
Parallelogram perimeter = 45 + 34 + 45 + 34
= 158 meters
36 meters
20 meters
Rectangle perimeter = 36 + 20 + 36 + 20
= 112 meters
It takes longer to maintain the parallelogram lawn because the perimeter is so much greater
and therefore takes longer to edge. Edward’s charges need to change so that lawn perimeter is
considered, too.
Same shape, different perimeters
Your friends ran into a similar problem back in Chapter 4 when they
were picking out a venue for the rock festival—the biggest field didn’t
necessarily have the most perimeter. For our lawn calculations, even if we
know the area of a particular lawn, we can’t make any assumptions about
its perimeter or how long it will take to edge the lawn. And currently,
Edward’s charges are only based on lawn area.
Same Area ≠ Same Perimeter
250 Chapter 6
quadrilaterals
Q:
So it’s not just triangles that have
perimeter?
A: No, not at all. The perimeter of a
shape is basically the edge around the
outside of a shape, whether it’s a triangle,
rectangle, parallelogram, or some other
shape.
Q:
Are there any shortcuts we can
take in calculating the perimeter of a
particular shape?
A:It all depends on the shape.
You calculate the perimeter of a shape by
adding the lengths of all its sides together.
You can take a few shortcuts if some of
these sides are the same length.
As an example, a square has four sides that
are all the same length, so the perimeter of
a square is just 4 times the length of one
side.
Q:
What about for a parallelogram?
A:A parallelogram has two pairs of
congruent sides, so there are two unique
side lengths. You can find the perimeter of
a parallelogram by adding these two unique
side lengths together, and then multiplying
by 2.
Q:
What if two shapes have the same
area and the same perimeter? Does this
mean they’re the same shape?
A:Not automatically, no, you need
more information. Many different shapes
can have the same area and the same
perimeter.
Q:
More information? Like what?
A:Well, a good starting point is if you
know what sort of shapes you’re dealing
with. This will tell you how many sides your
shapes have, and how many of these are
congruent.
As an example, if you’re told you have two
squares and they both have the same area,
the squares must be congruent. This is
because you calculate the area of a square
by calculating (side length)
2
. The only way
the squares can have the same area is if
their sides are the same length.
In general, if you know what type of shape
you’re dealing with, you can use the
properties of the shape to help you deduce
further facts.
A parallelogram is a four-sided shape Consecutive angles of a
whose opposite sides are parallel to parallelogram are supplementary.
each other.
To calculate parallelogram area,
Opposite sides of a parallelogram multiply the width by the height:
are congruent.
To calculate parallelogram perimeter,
Opposite angles of a parallelogram add together the length of each side.
are congruent.
you are here 4 251
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

