quadrilaterals
Use diagonals to find the area of the kite
Just like the parallelogram, there’s a shortcut we can take to find the area
of a kite. All we need to do is multiply the lengths of the two diagonals
together, and divide by 2:
Kite Area = 1/2 (diagonal 1 × diagonal 2)
Diagonal 1
Diagona
l 2
Diagona
l 2 is the base
1/2 Diagona
l 1
(the height)
How much should you charge for maintaining this lawn? We’ve
added in some extra measurements to help you.
Don’t forget that you’ll still need to edge round the flower bed,
even though you aren’t mowing it.
30 meters
20 meters
10.25 meters
3.75 meters
4.5 meters
13 meters
W
atch out f
or the flowers when
you’r
e edging, they’re exp
ensiv
e!.
you are here 4 257
sharpen solution
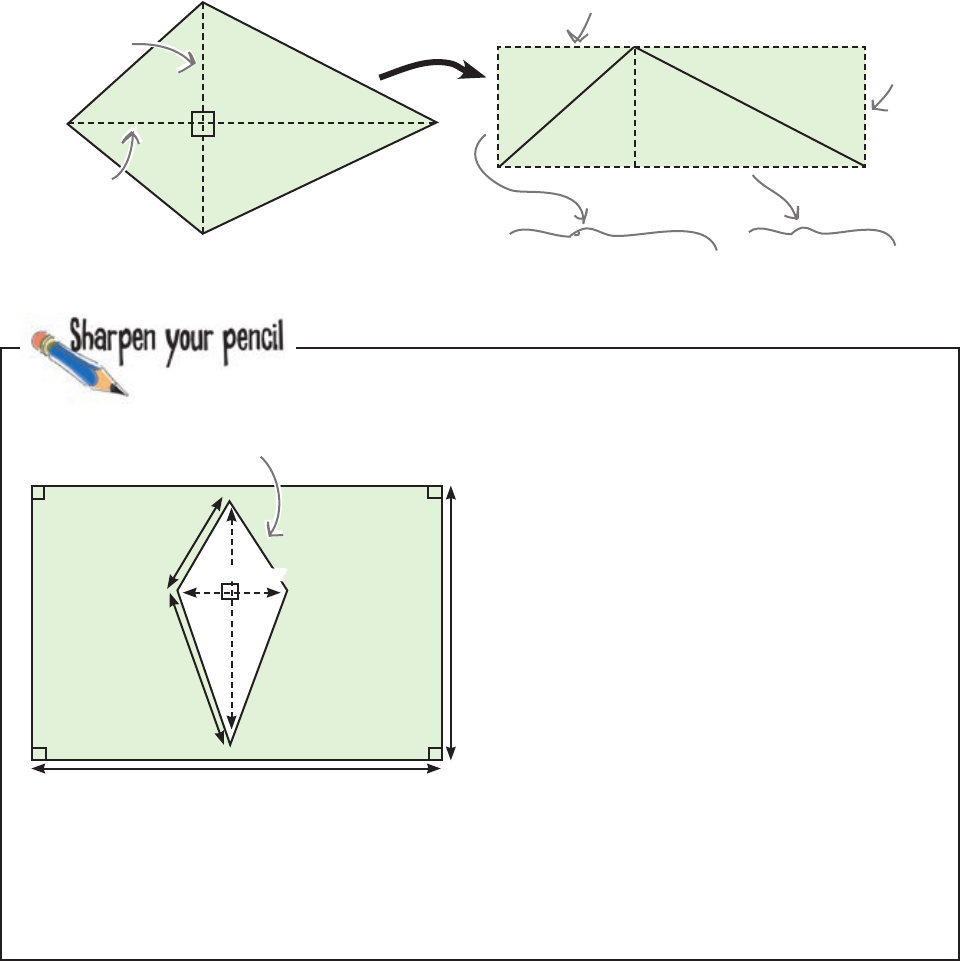
How much should you charge for maintaining the lawn? We’ve
added in some extra measurements to help you.
Don’t forget that you’ll still need to edge round the flower bed,
even though you aren’t mowing it.
30 meters
20 meters
10.25 meters
3.75 meters
4.5 meters
13 meters
Area of rectangle = 20 x 30
= 600 meters
2
Perimeter of rectangle = (2 x 20) + (2 x 30)
= 40 + 60
= 100 meters
Area of kite = 1/2 (4.5 x 13)
= 1/2 (58.5)
= 29.25 meters
2
Perimeter of kite = (2 x 3.75) + (2 x 10.25)
= 7.5 + 20.5
= 28 meters
Total area to maintain = 600 - 29.25
= 570.75 meters
2
Total perimeter to maintain = 100 + 28
= 128 meters
Total charge = $0.05 x 570.75 + $0.10 x 128
= $28.54 + $12.80
= $41.34
Round t
o 2
decima
l pl
ac
es.
258 Chapter 6
quadrilaterals
Kites Up Close
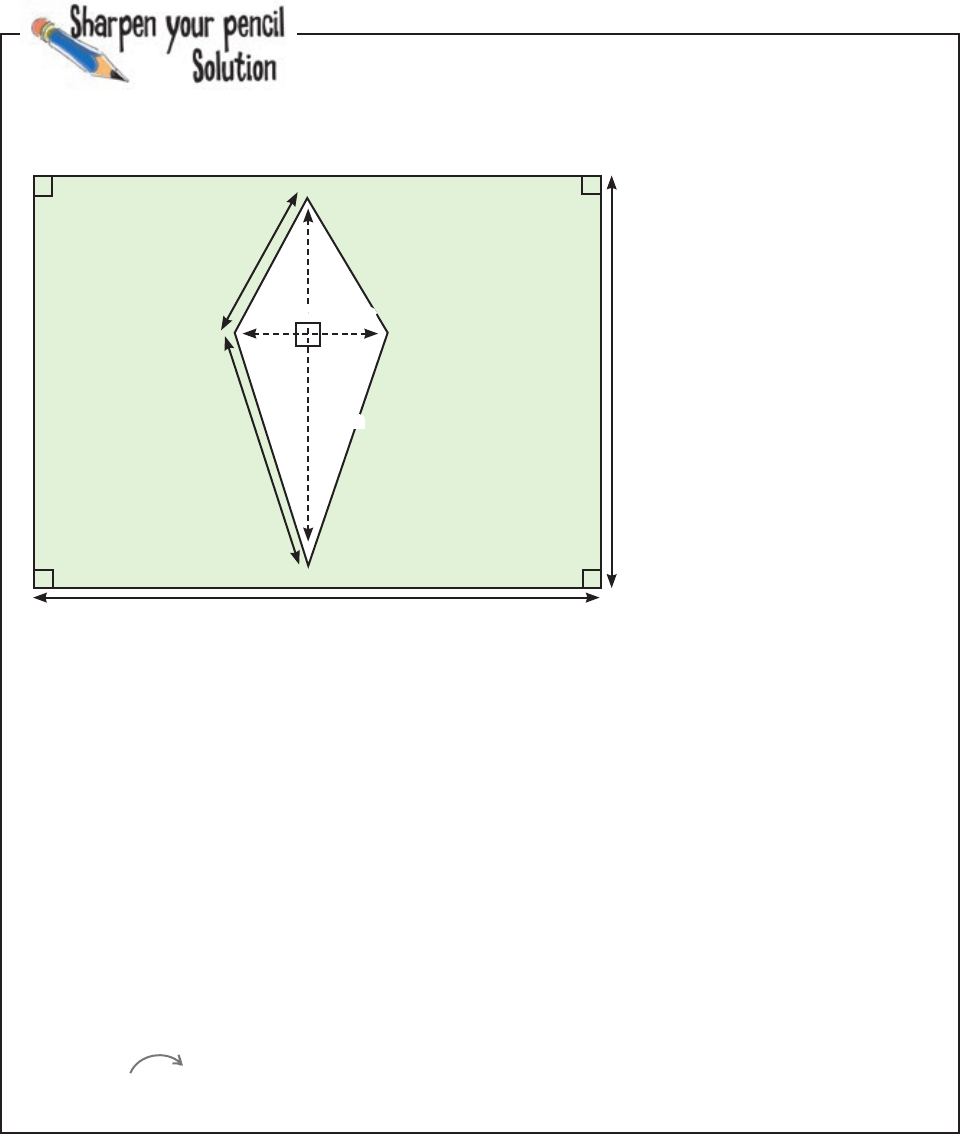
Diagonals
The diagonals of a kite are perpendicular,
but that’s not all there is to say about them.
For starters, one diagonal bisects the other,
meaning it chops the other diagonal in half.
It also bisects the pair of opposite angles, and
if you look at the remaining pair of angles,
they’re congruent, too. So there’s a lot you
can know about a kite without having to do
any calculations!
Area and perimeter
As you discovered earlier, you find the area of a kite by
multiplying together the lengths of the two diagonals and
dividing by two. To find the perimeter, remember that
there are two pairs of congruent sides so you only have to
add the two different sides together and multiply by two.
T
his diagona
l bisects
the other diagonal.
T
he diagona
l bisects
these angles, too.
T
hese angles ar
e congruent.
Q:
So the diagonals of a kite
are perpendicular. What about the
diagonals of a parallelogram, are they
perpendicular, too?
A:In general, parallelograms don’t have
perpendicular diagonals.
The diagonals of a parallelogram are
still important though. If a shape is a
parallelogram, then its diagonals bisect
each other. Try adding diagonals to the
parallelograms earlier in the chapter and
you’ll see what we mean.
Q:
Could I have calculated the area
of the kite by splitting it into simpler
shapes like before?
A:You could, but it would have taken
you much longer to calculate. All you really
need to do is multiply the two diagonals
together and divide the result by 2.
Q:
The kites we’ve looked at in this
chapter look symmetrical. Is that a
coincidence?
A:No, not at all. Every kite is
symmetrical along one diagonal.
Q:
Can a shape be both a
parallelogram and a kite?
A:Yes it can. A shape is a parallelogram
and a kite if it fits the description of both.
In other words, it must have two pairs of
separate adjacent congruent sides, and
also the opposing sides must be parallel.
This means that all four sides must be
congruent.
An example of a shape that is both a
parallelogram and a kite is a square. All four
sides are congruent, and opposite sides are
parallel. We’ll get to that in a little bit.…
you are here 4 259
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

