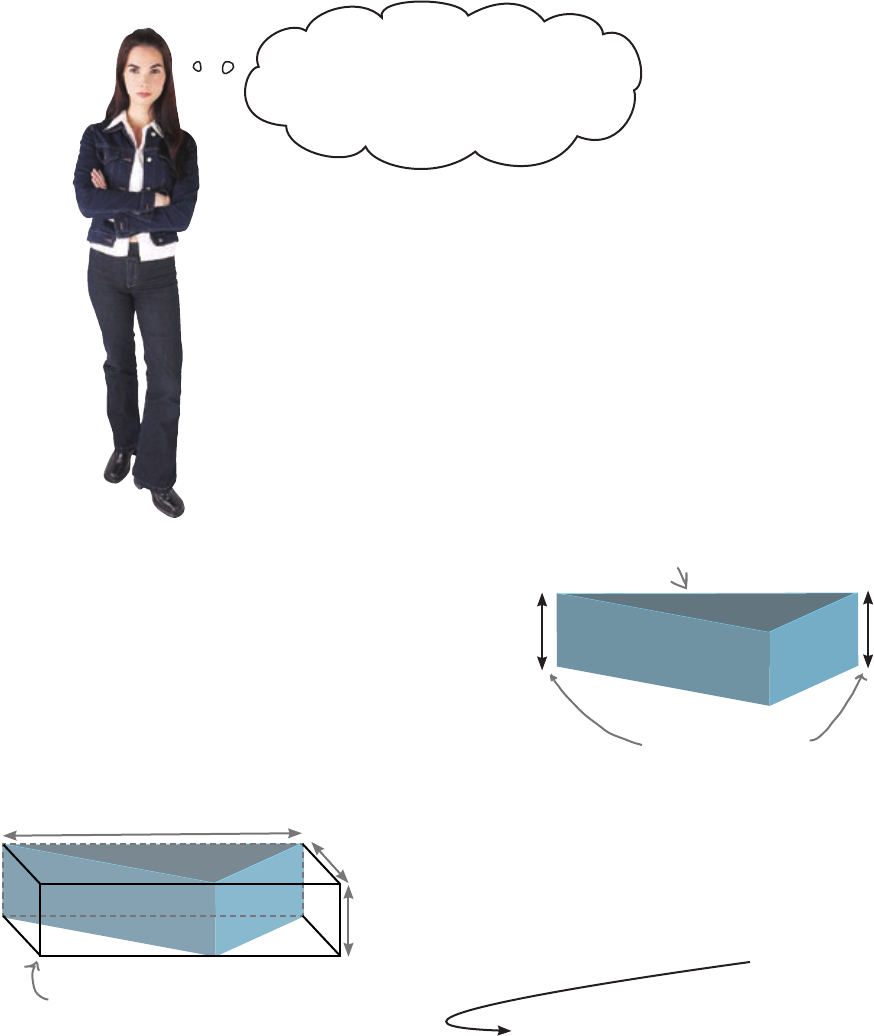
Length
T
hese “s
traight-sided” s
hap
es ar
e
known as prisms—mor
e about those
in Head Fir
st 3D Geometry.
W
idth
you know how to find area
Hot tub volume is area x depth
Calculating the volume of some 3D shapes can get pretty
gnarly, but for the hot tub range it’s simple. The tubs have
straight sides, so the volume can be found from area × depth.
[T
hank
s! Marketing xx]
AREA = length x width
Same depth a
ll ov
er
Q:
This book is called Head First 2D
Geometry, right? So how come we’re
talking about 3D in this chapter?
A:Volume is definitely a 3D topic, and
we cover it in much more detail in Head
First 3D Geometry, but it’s not too bad to
dip your toes in the water is it? Also, we’re
about to turn this problem back into a 2D
one on the next page.
Q:
You’re going to turn a 3D problem
into a 2D problem? How does that
work?
A:The third dimension in the hot tubs
problem is depth. Once we don’t have to
work with the depth anymore it’s just a 2D
problem we’re left with. Hold that thought
to the bottom of the next page.
Q:
What if the tub was deeper at
one end than the other? Or had curved
sides?
A:The area × depth formula only
applies to 3D shapes with straight sides, all
of the same depth, which are perpendicular
to the base. If the hot tub was deeper
at one end we’d need a different way of
working out its volume.
280 Chapter 7
regular polygons
Our complete summer range..
.
A
l
l
St
r
H
o
t T
ubs
T
r
i
-
c
u
z
i
C
h
i
l
l
-
ou
t
-
c
or
n
er
H
ex
-
i
t
-
u
p
7
t
h
H
eav
en R
el
ax
i
v
8
9
s
i
d
es
M
ag
i
c
C
i
r
c
l
e
T
ubs can be an
y size,
all depths 0.5m
Ok—so all the hot tubs
have the same depth. Does
that help simplify the
problem?
Yes. All the depths are the same, so only
the area of the hot tubs varies.
The All Star Hot Tubs range is a fixed depth: 0.5 meters.
You can have your tub wider and longer, but you can’t
have it deeper.
W
e know wha
t the depth
of any hot tub is.
The maximum volume allowed is 3 cubic meters, and all
the tubs are 0.5 meters deep. What’s the maximum area
our hot tub can have?
you are here 4 281
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

