90
Ha
nd dr
aw the
sun and r
ays
what does “the same” mean?
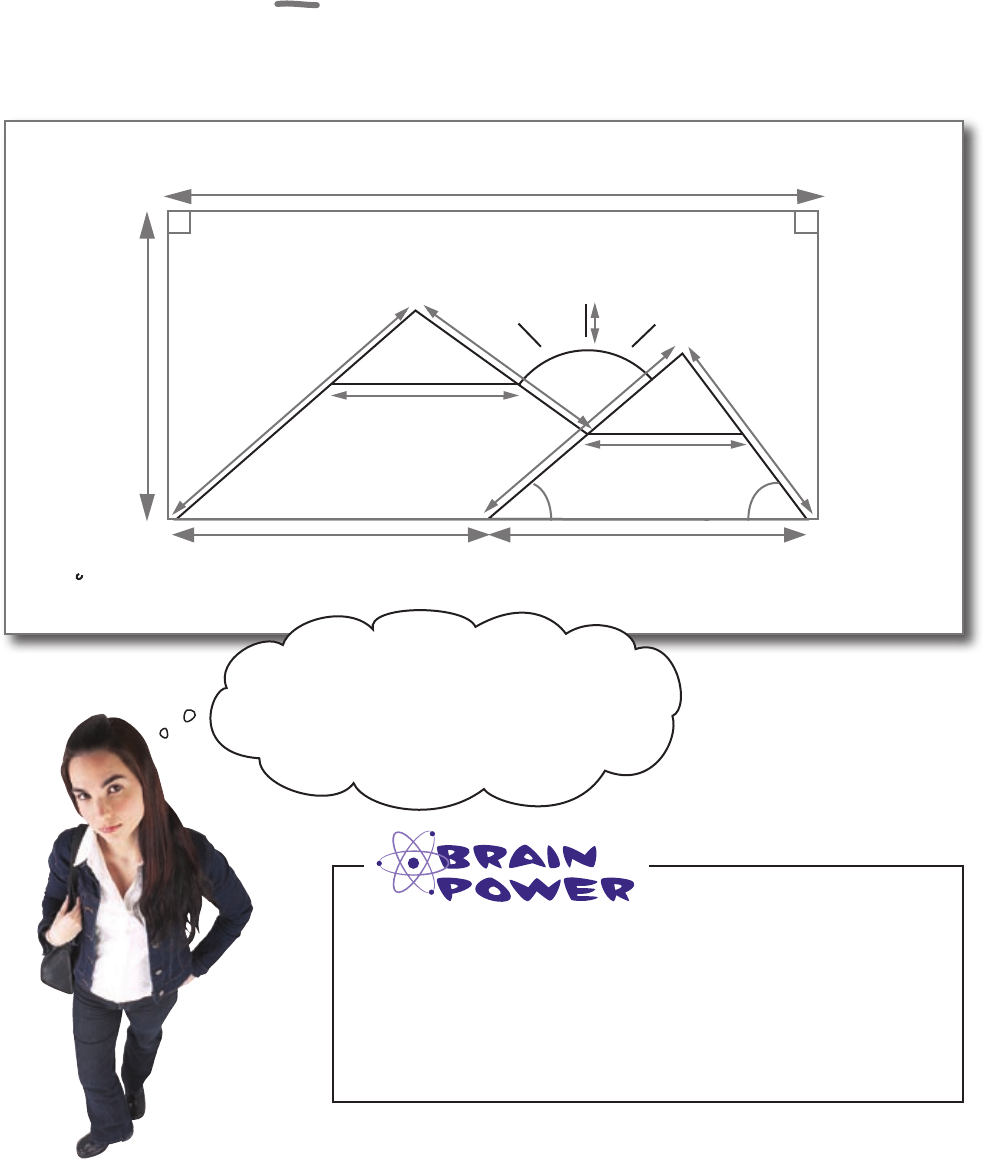
The design tells us that some triangles are repeated
120
The designer made a note saying that the two mountain
T
hese notes ar
e a big hint
about the missing informa
tion.
6060
37.5
30
40
48
40
6
60
41º 53º
This corner a
lso
Mou
ntain
tip tria
ngle
is the same
shape
tria
ngle as
the whole
mou
ntain
T
h
e
t
w
o
m
o
u
n
t
a
i
n
t
ri
a
n
g
le
s
a
r
e
t
h
e
s
a
m
e
s
h
a
p
e
,
bu
t
r
e
s
c
ale
d/flipped
56
triangles are the same but rescaled, or different sizes.
There’s also a note saying that the mountain tip is the same
triangle as the whole mountain.
But what exactly does he mean by “the same triangle”?
same?
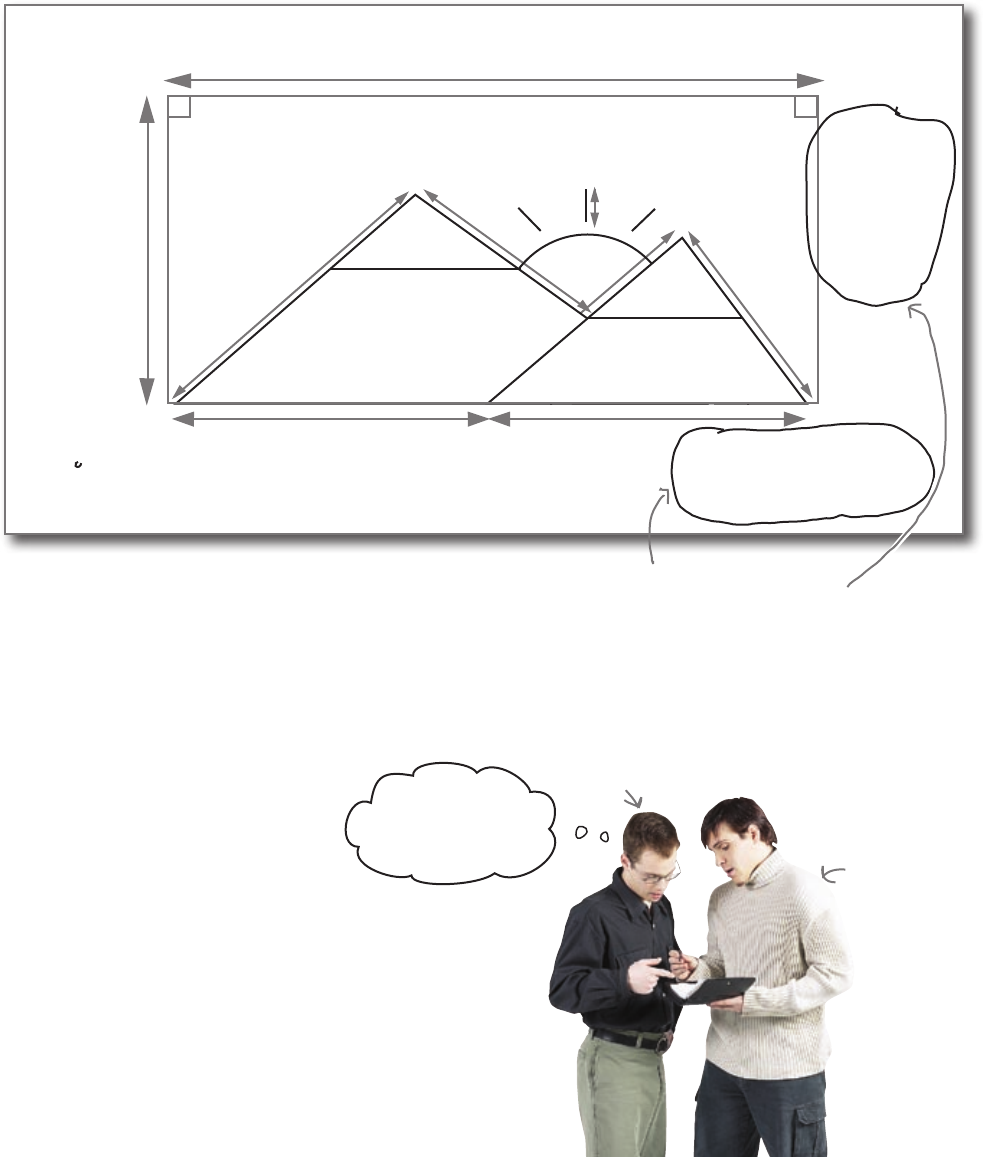
Jim: Yeah, I mean, the designer is talking nonsense. One of
them is bigger than the other. How on earth can they be the
Frank: Well, maybe he was talking about angles. Can you have
two triangles with the same angles but with different lengths?
Same triangle?
I don’t get what
this means.
Frank
Jim
54 Chapter 2
Jim
similarity and congruence
GEOMETRY Construction
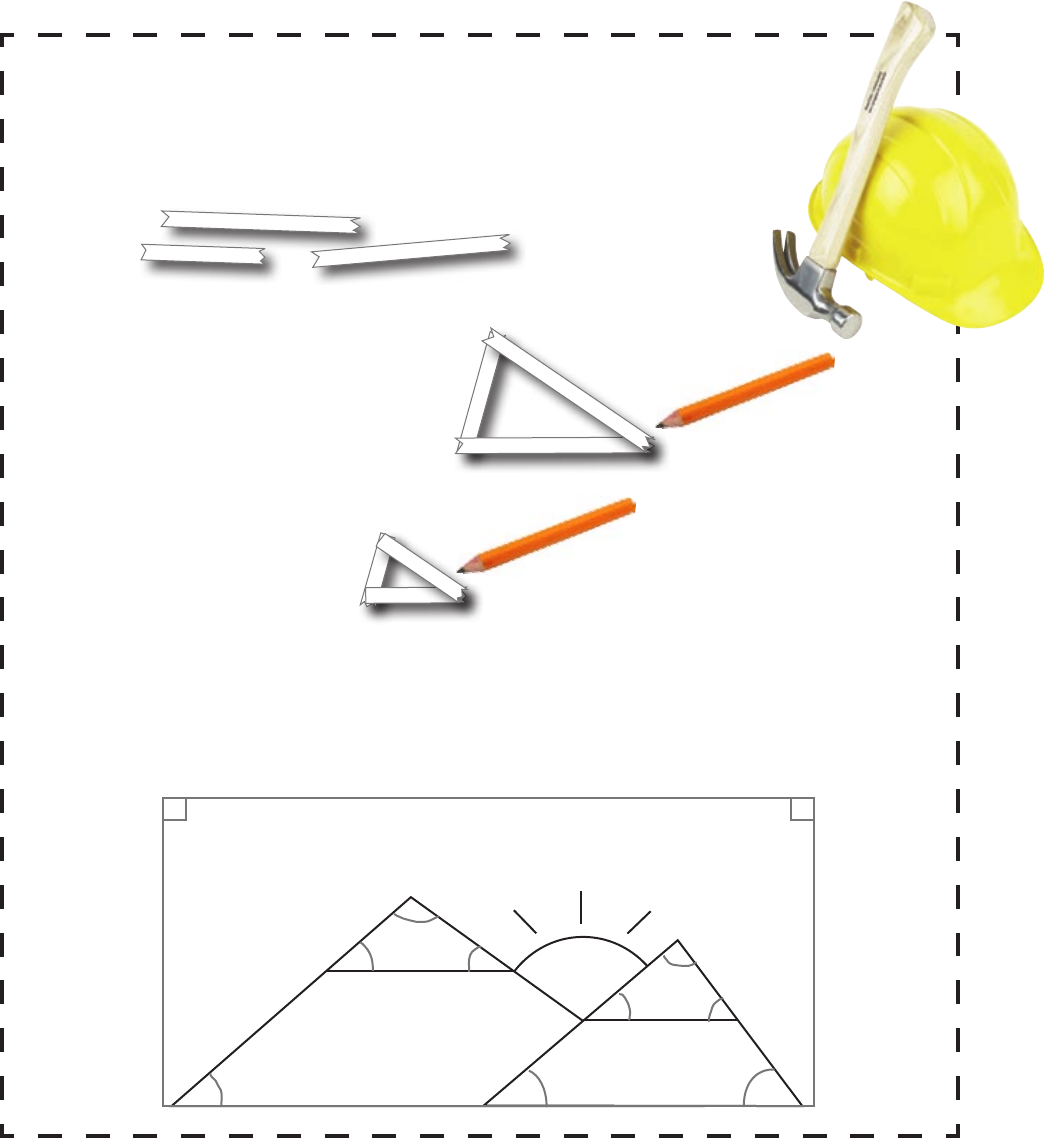
Can you have two triangles with the same angles but with different lengths?
1) Cut or tear three narrow strips of paper, making them slightly different lengths.
2) Make them into a triangle and draw around it on some scrap paper.
3) Now fold each of your strips of paper in half, join them up to make a triangle again, and draw around it.
Compare your drawings to investigate what happens to the angles of a triangle when you make it bigger or
smaller—you just need to make sure that you do the same to each side of your triangle.
Does your investigation help you to fill in any of the mystery angles on the design?
41º 53º
?
??
?
?
?
?
you are here 4 55
geometry construction solution
GEOMETRY Construction SOLUTION
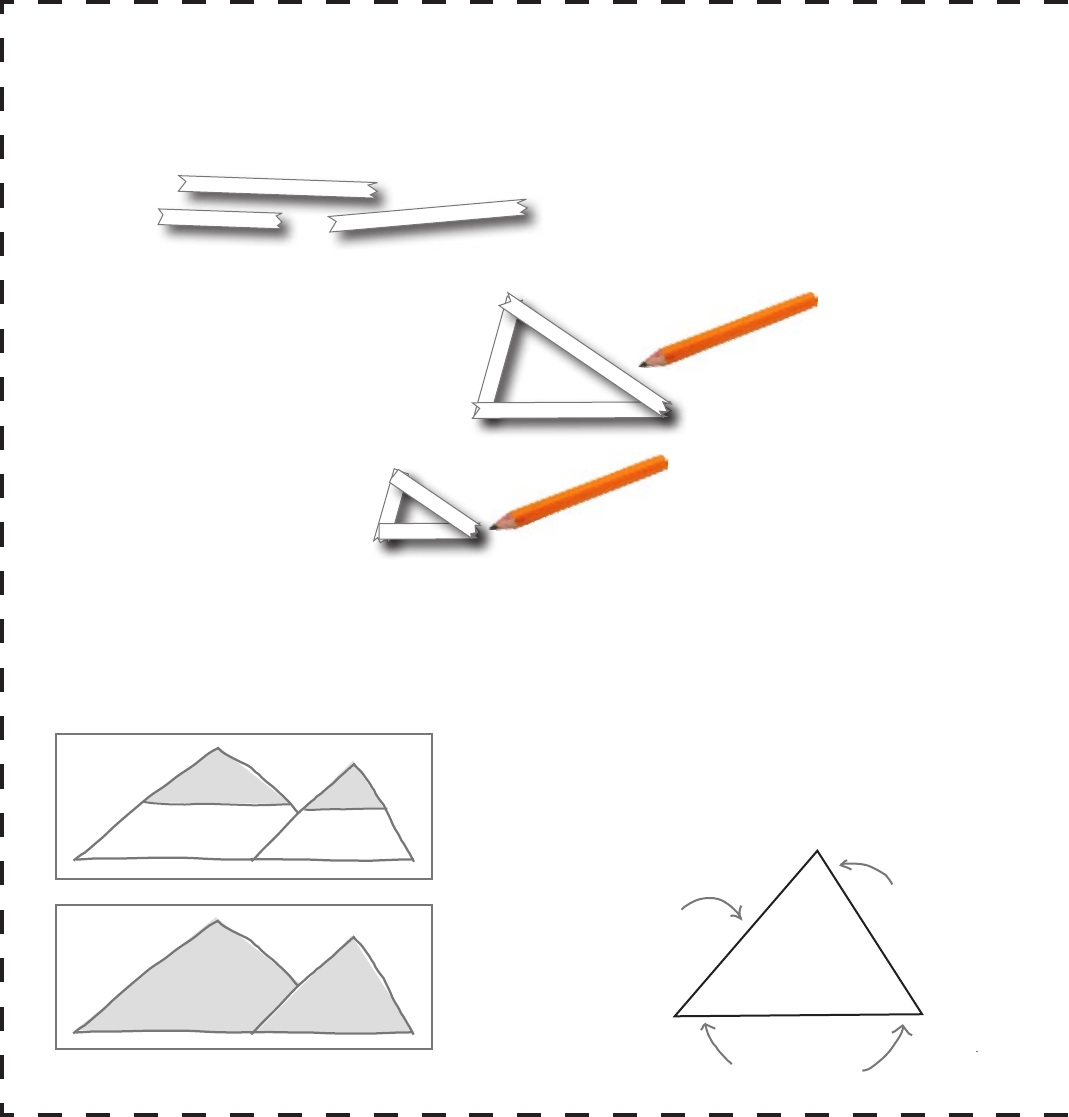
Can you have two triangles with the same angles but with different lengths?
1) Cut or tear three narrow strips of paper, making them slightly different lengths.
2) Make them into a triangle and draw around it on some scrap paper.
3) Now fold each of your strips of paper in half, join them up to make a triangle again, and draw around it.
Compare your drawings to investigate what happens to the angles of a triangle when you make it bigger or
smaller—you just need to make sure that you do the same to each side of your triangle.
Does your investigation help you to fill in any of the mystery angles on the design?
?
53°
41°
C
hanging the size of the
triangle doesn’t change
the angles.... So each
triangle mus
t hav
e the
same angles as this one.
W
e don’t know
this angle.
We know these
t
w
o angles.
Making a triangle bigger or smaller doesn’t change the angles of the corners—
providing you change the length of all the sides by the same ratio.
The mountains are basically made out of 4 of
the same triangle in different sizes (one tucks in
the back but the other corners are the same).
1
2
3
4
56 Chapter 2
GEOMETRY Construction SOLUTION
similarity and congruence
you are here 4 57
Hold on—didn’t you spend Chapter 1
going on about how we couldn’t trust our
eyes to tell us if things looked right?
Now you’re saying these triangles are
“similar”? Sounds flaky to me—what’s the
deal?
180
o
in a tr
iangle
(180
o
-(41
o
+ 53
o
) = 86
o
F
ir
s
t find the missing
angle in the tr
iangle…
…and then copy those angles t
o
a
ll f
our of the tr
iangles, as w
e
know they’r
e a
ll the same.
T
he f
our triangles have the same
angles because they’re simil
ar.
86°
53°
41°
41º 53º
86º
86º
41º
41º
41º
53º
53º
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

